题目内容
求下列图形中各阴影部分的面积.(图中单位:厘米)


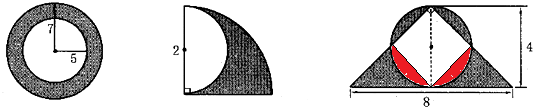
分析:(1)根据圆环的面积=π(R2-r2),代入数据即可解答;
(2)阴影部分的面积等于半径2厘米的
圆的面积减去直径2厘米的半圆的面积;
(3)如图,上部的两个阴影部分的面积正好等于下面红色部分的面积,则阴影部分的面积就等于底为8,高为4÷2=2的三角形的面积,据此计算即可;
(2)阴影部分的面积等于半径2厘米的
| 1 |
| 4 |
(3)如图,上部的两个阴影部分的面积正好等于下面红色部分的面积,则阴影部分的面积就等于底为8,高为4÷2=2的三角形的面积,据此计算即可;

解答:解:(1)3.14×(72-52)
=3.14×(49-25)
=3.14×24
=75.36(平方厘米)
(2)
×3.14×22-3.14×(2÷2)2÷2
=3.14-1.57
=1.57(平方厘米)
(3)8×4÷2÷2=8(平方厘米).
=3.14×(49-25)
=3.14×24
=75.36(平方厘米)
(2)
| 1 |
| 4 |
=3.14-1.57
=1.57(平方厘米)
(3)8×4÷2÷2=8(平方厘米).
点评:此题主要考查组合图形的面积的计算方法,利用等积变形转化不规则图形的面积是解决此类问题的关键.

练习册系列答案
相关题目