题目内容
求下列图形中涂色部分的面积.
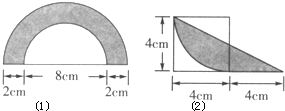

分析:(1)由图意可知:阴影部分的面积就等于半个圆环的面积,利用环形的面积公式S=π×(R2-r2),即可得解;
(2)如图所示,三角形ABC和三角形ABD等底等高,则二者的面积相等,它们都去掉公共部分三角形ABE,那么剩余的部分仍然相等,即三角形BCE和三角形ADE的面积相等,于是阴影部分就转化成了以正方形的边长为半径的
圆,于是利用圆的面积公式即可求解.

(2)如图所示,三角形ABC和三角形ABD等底等高,则二者的面积相等,它们都去掉公共部分三角形ABE,那么剩余的部分仍然相等,即三角形BCE和三角形ADE的面积相等,于是阴影部分就转化成了以正方形的边长为半径的
| 1 |
| 4 |

解答:解:(1)8÷2=4(厘米),
4+2=6(厘米),
3.14×(62-42)÷2,
=3.14×(36-16)÷2,
=3.14×20÷2,
=31.4(平方厘米);
答:阴影部分的面积是31.4平方厘米.
(2)
×3.14×42,
=3.14×4,
=12.56(平方厘米);
答:阴影部分的面积是12.56平方厘米.
4+2=6(厘米),
3.14×(62-42)÷2,
=3.14×(36-16)÷2,
=3.14×20÷2,
=31.4(平方厘米);
答:阴影部分的面积是31.4平方厘米.
(2)
| 1 |
| 4 |
=3.14×4,
=12.56(平方厘米);
答:阴影部分的面积是12.56平方厘米.
点评:(1)此题主要考查环形的面积的计算方法的灵活应用.
(2)将阴影部分转化成
圆,是解答本题的关键.
(2)将阴影部分转化成
| 1 |
| 4 |

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
