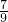题目内容
如果一个长方形两条相邻的边都增加它们的
，那么所得的长方形的面积比原来增加了原来面积的（ ）
| 1 |
| 3 |
分析：设原来的长方形的长和宽分别为a和b，则变化后的长方形的长和宽分别为（1+
）a、（1+
）b，利用长方形的面积公式分别求出变化前后的面积，即可求出面积增加的分率．
| 1 |
| 3 |
| 1 |
| 3 |
解答：解：设原来的长方形的长和宽分别为a和b，则变化后的长方形的长和宽分别为（1+
）a、（1+
）b，
原来的面积：ab，
现在的面积：（1+
）a×（1+
）b，
=
a×
b，
=
ab；
面积增加：（
-1）ab÷ab，
=
ab÷ab，
=
；
答：所得的长方形的面积比原来增加了原来面积的
．
故选：D．
| 1 |
| 3 |
| 1 |
| 3 |
原来的面积：ab，
现在的面积：（1+
| 1 |
| 3 |
| 1 |
| 3 |
=
| 4 |
| 3 |
| 4 |
| 3 |
=
| 16 |
| 9 |
面积增加：（
| 16 |
| 9 |
=
| 7 |
| 9 |
=
| 7 |
| 9 |
答：所得的长方形的面积比原来增加了原来面积的
| 7 |
| 9 |
故选：D．
点评：此题主要考查长方形的面积的计算方法的灵活应用．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
，那么所得的长方形的面积比原来增加了原来面积的
