题目内容
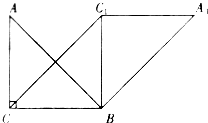 如图,在直角三角形ABC中,∠ACB=90°,AC=BC=10,将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1.
如图,在直角三角形ABC中,∠ACB=90°,AC=BC=10,将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1.
(1)线段A1C1的长度是______,∠CBA1的度数是______.
(2)连结CC1,求证:四边形CBA1C1是平行四边形.
(1)解:因为将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1.
所以A1C1=10,∠CBC1=90°,
而△ABC是等腰直角三角形,
所以∠A1BC1=45°,
所以∠CBA1=135°;
(2)证明:因为∠A1C1B=∠C1BC=90°,
所以A1C1∥BC.
又因为A1C1=AC=BC,
所以四边形CBA1C1是平行四边形.
分析:(1)由于将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1,根据旋转的性质可以得到A1C1=AC,∠CBC1=90°,而△ABC是等腰直角三角形,利用等腰直角三角形的性质即可求出∠CBA1的度数;
(2)由∠A1C1B=∠C1BC=90°可以得到A1C1∥BC,又A1C1=AC=BC,利用评选四边形的判定即可证明题目的问题.
点评:此题主要考查了旋转的性质,也考查了平行四边形的判定,解题的关键是利用旋转的性质得到相等的相等和相等的角,然后利用等腰直角三角形的性质加减问题.
所以A1C1=10,∠CBC1=90°,
而△ABC是等腰直角三角形,
所以∠A1BC1=45°,
所以∠CBA1=135°;
(2)证明:因为∠A1C1B=∠C1BC=90°,
所以A1C1∥BC.
又因为A1C1=AC=BC,
所以四边形CBA1C1是平行四边形.
分析:(1)由于将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1,根据旋转的性质可以得到A1C1=AC,∠CBC1=90°,而△ABC是等腰直角三角形,利用等腰直角三角形的性质即可求出∠CBA1的度数;
(2)由∠A1C1B=∠C1BC=90°可以得到A1C1∥BC,又A1C1=AC=BC,利用评选四边形的判定即可证明题目的问题.
点评:此题主要考查了旋转的性质,也考查了平行四边形的判定,解题的关键是利用旋转的性质得到相等的相等和相等的角,然后利用等腰直角三角形的性质加减问题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
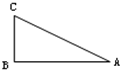 如图:在直角三角形中,∠A=28°,∠C=
如图:在直角三角形中,∠A=28°,∠C=
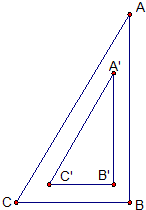 如图,在直角三角形ABC中,∠ABC=90°,ABPA′B′,BCPB′C′,ACPA′C′,且三对平行线的距离都是1,若AC=10,AB=8,BC=6,求三角形A′B′C′上的点到三角形ABC三边距离的最大值.
如图,在直角三角形ABC中,∠ABC=90°,ABPA′B′,BCPB′C′,ACPA′C′,且三对平行线的距离都是1,若AC=10,AB=8,BC=6,求三角形A′B′C′上的点到三角形ABC三边距离的最大值.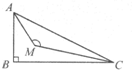 如图,在直角三角形ABC中,AM、CM分别平分∠A、∠C,则∠M是
如图,在直角三角形ABC中,AM、CM分别平分∠A、∠C,则∠M是 如图:在直角三角形中,∠A=28°,∠C=________°.
如图:在直角三角形中,∠A=28°,∠C=________°.