题目内容
 在右边的竖式中,相同字母代表相同数字,不同字母代表不同数字,则四位数
在右边的竖式中,相同字母代表相同数字,不同字母代表不同数字,则四位数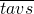 =________.
=________.
1038
分析:本题可以直接想整数的加法的计算法则:先算个位,再算十位,再算百位,最后算千位.同时每次计算满十向前一位进一.从而推算出每个数位上字母代表哪个数字,最后得出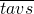 的得数.
的得数.
解答:由题意(1)从竖式中个位数a加t等于t可以知道a=0;
因为假设a≠0,则 a+t=10+t 计算可得a=10,
根据整数的性质和加法计算法则可知:a不可能等于10.
所以a=0.
(2)同理可得:t=1.
因为假设t≠1,t=2 则竖式中千位上的数s+v的值是22,即s和v大于9,竖式不成立.
所以t=1.
(3)十位上的数v+s得数有两种可能:
①v+s=t 或 ②v+s=10+t;
由t=1,可知①v+s=t不成立.即
②v+s=10+t成立,v+s=11,则竖式的百位上相加是:
t+t+1=v,计算可得,v=3;
因为v+s=11,v=3,所以s=11-3=8
(4)由以上条件:a=0,t=1,v=3,s=8 得解,四位数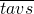 ═1038
═1038
故答案为:1038.
点评:本题非常巧妙地考察了考生对整数的加法运算法则及数位的进位、零的认识性质等知识要点的熟悉掌握程度.
分析:本题可以直接想整数的加法的计算法则:先算个位,再算十位,再算百位,最后算千位.同时每次计算满十向前一位进一.从而推算出每个数位上字母代表哪个数字,最后得出
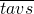 的得数.
的得数.解答:由题意(1)从竖式中个位数a加t等于t可以知道a=0;
因为假设a≠0,则 a+t=10+t 计算可得a=10,
根据整数的性质和加法计算法则可知:a不可能等于10.
所以a=0.
(2)同理可得:t=1.
因为假设t≠1,t=2 则竖式中千位上的数s+v的值是22,即s和v大于9,竖式不成立.
所以t=1.
(3)十位上的数v+s得数有两种可能:
①v+s=t 或 ②v+s=10+t;
由t=1,可知①v+s=t不成立.即
②v+s=10+t成立,v+s=11,则竖式的百位上相加是:
t+t+1=v,计算可得,v=3;
因为v+s=11,v=3,所以s=11-3=8
(4)由以上条件:a=0,t=1,v=3,s=8 得解,四位数
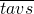 ═1038
═1038故答案为:1038.
点评:本题非常巧妙地考察了考生对整数的加法运算法则及数位的进位、零的认识性质等知识要点的熟悉掌握程度.

练习册系列答案
相关题目
 在右边的加法竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字.如果“纪”=3,那么“北京奥运新世纪”七个字的乘积是
在右边的加法竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字.如果“纪”=3,那么“北京奥运新世纪”七个字的乘积是 在右边的竖式中,相同字母代表相同数字,不同字母代表不同数字,则四位数
在右边的竖式中,相同字母代表相同数字,不同字母代表不同数字,则四位数