题目内容
如图，已知D是BC上一点，∠C=62°，∠CAD=32°，则∠ADB=________度．
94
分析：因则∠ADB和∠ADC组成了一个平角，根据三角形的内角和等于180度，可求出∠ADC的度数．据此解答．
解答：∠ADC=180°-∠C-∠CAD，
∠ADC=180°-62°-32°，
∠ADC=86°，
∠ADB=180°-∠ADC，
∠ADB=180°-86°，
∠ADB=94°．
答：∠ADB=94度．
故答案为：94．
点评：本题的关键是根据三角形的内角和是180度，求出∠ADC的度数．
分析：因则∠ADB和∠ADC组成了一个平角，根据三角形的内角和等于180度，可求出∠ADC的度数．据此解答．
解答：∠ADC=180°-∠C-∠CAD，
∠ADC=180°-62°-32°，
∠ADC=86°，
∠ADB=180°-∠ADC，
∠ADB=180°-86°，
∠ADB=94°．
答：∠ADB=94度．
故答案为：94．
点评：本题的关键是根据三角形的内角和是180度，求出∠ADC的度数．
练习册系列答案
智慧小复习系列答案
相关题目
如图所示，A至B是下坡，B至C是平路，C至D是上坡．小张和小王在上坡时步行速度是每小时4千米，平路时步行速度是每小时5千米，下坡时步行速度是每小时6千米．小张和小王分别从A和D同时出发，1小时后两人在E点相遇．已知E在BC上，并且E至C的距离是B至C距离的
如图，A至B是下坡，B至C是平路，C至D是上坡．小张和小王在上坡时步行速度是每小时4千米，平路时步行速度是每小时5千米，下坡时步行速度是每小时6千米．小张和小王分别从A和D同时出发，2小时后两人在E点相遇．已知E在BC上，并且E至C的距离是B至C距离的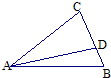
如图，已知D是BC上一点，∠C=62°，∠CAD=32°，则∠ADB=
如图所示，A至B是下坡，B至C是平路，C至D是上坡．小张和小王在上坡时步行速度是每小时4千米，平路时步行速度是每小时5千米，下坡时步行速度是每小时6千米．小张和小王分别从A和D同时出发，1小时后两人在E点相遇．已知E在BC上，并且E至C的距离是B至C距离的
．当小王到达A后9分钟，小张到达D．那么A至D全程长是多少千米？