题目内容
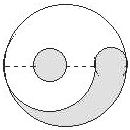 如图,图中的曲线是用半径长度的比为2:1.5:0.5的6条半圆曲线连成的.问:涂有阴影的部分与未涂阴影的部分的面积比是多少?
如图,图中的曲线是用半径长度的比为2:1.5:0.5的6条半圆曲线连成的.问:涂有阴影的部分与未涂阴影的部分的面积比是多少?分析:根据圆的面积公式分别得到涂有阴影的部分与未涂阴影的部分的面积,再求出它们的比即可.
解答:解:涂有阴影的部分的面积为:
π×(0.5r)2×1.5+[π×(2r)2×0.5-π×(1.5r)2×0.5],
=
πr2+[2πr2-
πr2],
=
πr2+
πr2,
=
πr2,
未涂阴影的部分的面积为:
π×(2r)2-
πr2,
=4πr2-
πr2,
=
πr2,
πr2:
πr2=
.
答:涂有阴影的部分与未涂阴影的部分的面积比是
.
π×(0.5r)2×1.5+[π×(2r)2×0.5-π×(1.5r)2×0.5],
=
| 3 |
| 8 |
| 9 |
| 8 |
=
| 3 |
| 8 |
| 7 |
| 8 |
=
| 5 |
| 4 |
未涂阴影的部分的面积为:
π×(2r)2-
| 5 |
| 4 |
=4πr2-
| 5 |
| 4 |
=
| 11 |
| 4 |
| 11 |
| 4 |
| 5 |
| 4 |
| 11 |
| 5 |
答:涂有阴影的部分与未涂阴影的部分的面积比是
| 11 |
| 5 |
点评:考查了圆的面积和比的意义,本题关键是得到涂有阴影的部分的面积和未涂阴影的部分的面积.

练习册系列答案
相关题目
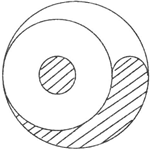 如图中的曲线是用半径长度的比为4:3:1的7条半圆曲线连成的.涂有阴影的部分与未涂阴影部分的面积比是多少?
如图中的曲线是用半径长度的比为4:3:1的7条半圆曲线连成的.涂有阴影的部分与未涂阴影部分的面积比是多少?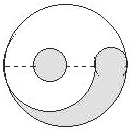 如图,图中的曲线是用半径长度的比为2:1.5:0.5的6条半圆曲线连成的.问:涂有阴影的部分与未涂阴影的部分的面积比是多少?
如图,图中的曲线是用半径长度的比为2:1.5:0.5的6条半圆曲线连成的.问:涂有阴影的部分与未涂阴影的部分的面积比是多少?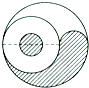 如图中的曲线是用半径长度的比为4:3:1的7条半圆曲线连成的.涂有阴影的部分与未涂阴影部分的面积比是多少?
如图中的曲线是用半径长度的比为4:3:1的7条半圆曲线连成的.涂有阴影的部分与未涂阴影部分的面积比是多少?