题目内容
(2010?湖北模拟)在如图所示的长方形ABCO中,三角形ABD的面积比三角形BCD的面积大10平方厘米,求阴影部分的面积.
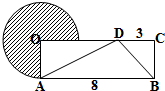

分析:由图可以看出:三角形ABD与三角形BCD等高不等底,则其面积比即为其底的比,即S△ABD:S△BCD=8:3,再由二者的面积相差10平方厘米,就可求出他们的高,也就是长方形的宽,又是圆的半径,从而能求圆的面积.阴影部分占圆的
,问题得解.
| 3 |
| 4 |
解答:解:因S△ABD:S△BCD=8:3,S△ABD-S△BCD=10,
所以可以设S△BCD为x,则S△ABD为
x,
x-x=10,
x=10,
x=6;
CB=6×2÷3=4(厘米),
阴影的面积=
πr2=
×3.14×42=37.68(平方厘米);
答:阴影部分的面积是37.68平方厘米.
所以可以设S△BCD为x,则S△ABD为
| 8 |
| 3 |
| 8 |
| 3 |
| 5 |
| 3 |
x=6;
CB=6×2÷3=4(厘米),
阴影的面积=
| 3 |
| 4 |
| 3 |
| 4 |
答:阴影部分的面积是37.68平方厘米.
点评:此题主要考查三角形和圆的面积公式,关键是找出三角形的面积比,求圆的半径.

练习册系列答案
相关题目
 (2010?湖北模拟)如图是正方形的面积是6平方厘米,这个圆的面积是
(2010?湖北模拟)如图是正方形的面积是6平方厘米,这个圆的面积是