题目内容
 如图所示,两个正方形ABCD和DEFG的边长都是整数厘米,点E在线段CD上,且CE<DE,线段CF=5厘米,则五边形ABCFG的面积等于
如图所示,两个正方形ABCD和DEFG的边长都是整数厘米,点E在线段CD上,且CE<DE,线段CF=5厘米,则五边形ABCFG的面积等于71
71
平方厘米.分析:本题需要结合勾股定理,△CEF为直角三角形,因为CF=5厘米,且已知两个正方形ABCD和DEFG的边长都是整数厘米,因此CE=3厘米,EF=DE=4厘米,CD=7厘米,由此,五边形ABCFG的面积就等于边长分别为4厘米、7厘米的正方形的面积加上底和高分别为4厘米、3厘米的三角形的面积,利用正方形及三角形的面积公式代入数值求解即可.
解答:解:CF=5,又CD和DF都是整数,根据勾股定理可知CE=3厘米,EF=DE=4厘米,CD=7厘米,
所以五边形ABCFG的面积为:42+72+
×4×3
=16+49+6
=71(平方厘米);
答:五边形ABCFG的面积等于71平方厘米.
故答案为:71.
所以五边形ABCFG的面积为:42+72+
| 1 |
| 2 |
=16+49+6
=71(平方厘米);
答:五边形ABCFG的面积等于71平方厘米.
故答案为:71.
点评:本题解决的关键是利用勾股定理及题干要求判断出各图形的边长.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 如图所示有两个正方形.小正方形的边长为1,大正方形的边长为7.则AB长为
如图所示有两个正方形.小正方形的边长为1,大正方形的边长为7.则AB长为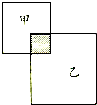 如图所示,两个正方形叠放在一起,阴影部分的面积是甲正方形的
如图所示,两个正方形叠放在一起,阴影部分的面积是甲正方形的 如图所示有两个正方形.小正方形的边长为1,大正方形的边长为7.则AB长为________.
如图所示有两个正方形.小正方形的边长为1,大正方形的边长为7.则AB长为________. 如图所示,两个正方形叠放在一起,阴影部分的面积是甲正方形的
如图所示,两个正方形叠放在一起,阴影部分的面积是甲正方形的 ,是乙正方形的
,是乙正方形的 .那么两正方形面积的比是多少?
.那么两正方形面积的比是多少?