题目内容
阅读下面的材料:
=1-
;
=
-
;
=
-
…
所以
+
+
=1-
+
-
+
-
=1-
=
根据上面的规律解答下面的问题:
(1)
+
+
+…+
=
(2)
+
+
+…+
=
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
所以
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
根据上面的规律解答下面的问题:
(1)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 10×11 |
| 10 |
| 11 |
| 10 |
| 11 |
(2)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n×(n+1) |
| n |
| n+1 |
| n |
| n+1 |
分析:根据给出的例子,如果分子为1,、分母为两个自然数的乘积,那么这个分数就可以拆分成两个分数相减的形式,然后通过加减相抵消的方法,解决问题.
解答:解:(1)
+
+
+…+
,
=1-
+
-
+
-
…+
-
,
=1-
,
=
;
(2)
+
+
+…+
,
=1-
+
-
+
-
…+
-
,
=1-
,
=
;
故答案为:
,
.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 10×11 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 10 |
| 1 |
| 11 |
=1-
| 1 |
| 11 |
=
| 10 |
| 11 |
(2)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n×(n+1) |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
故答案为:
| 10 |
| 11 |
| n |
| n+1 |
点评:此题中的每个分数形如
=
-
.
| 1 |
| a×(a+1) |
| 1 |
| a |
| 1 |
| a+1 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


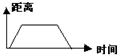 B.
B.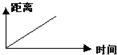 C.
C.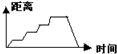 D.
D.