Question

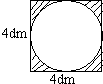画出图形的对称轴，并求出阴影部分面积．

Answer 1

分析：（1）依据轴对称图形的概念，即在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线就是其对称轴，从而画出图形的对称轴．
（2）由题意可知：阴影部分的面积=正方形的面积-圆的面积，圆的直径等于正方形的边长，正方形的边长已知，从而可以分别求出正方形和圆的面积，进而求出阴影部分的面积．

解答：解：（1）如图所示，即为图形的对称轴：
；

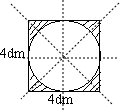（2）阴影部分的面积=4×4-3.14×(

4

2

)2，
=16-3.14×4，
=16-12.56，
=3.44（平方分米）；
答：阴影部分的面积是3.44平方分米．

点评：（1）依据轴对称图形的概念以及其轴对称图形的条数，即可画出其对称轴．
（2）此题主要考查正方形和圆的面积的计算方法，关键是明白：圆的直径等于正方形的边长．