题目内容
【题目】在边长为1的正方形内任取51个点,求证:一定可以从中找出3点,以它们为顶点的三角形的面积不大于1/50.
【答案】
【解析】
试题分析:将边长为1的正方形分成25个边长为![]() 的正方形,在51个点中,一定有[51÷25]+1=3(个)点属于同一个小正方形; 不妨设A、B、C三点边长为
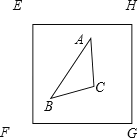
的正方形,在51个点中,一定有[51÷25]+1=3(个)点属于同一个小正方形; 不妨设A、B、C三点边长为![]() 三角形在小正方形EFGH内,由于三角形ABC的面积不大于小正方形面积EFGH的
三角形在小正方形EFGH内,由于三角形ABC的面积不大于小正方形面积EFGH的![]() ,又EFGH的面积为
,又EFGH的面积为![]() ×
×![]() =
=![]() ;故三角形ABC的面积不大于
;故三角形ABC的面积不大于![]() ;
;
解:将边长为1的正方形分成25个边长为![]() 的正方形,在51个点中,一定有[51÷25]+1=3(个)点属于同一个小正方形; 不妨设A、B、C三点边长为
的正方形,在51个点中,一定有[51÷25]+1=3(个)点属于同一个小正方形; 不妨设A、B、C三点边长为![]() 三角形在小正方形EFGH内,由于三角形ABC的面积不大于小正方形面积EFGH的
三角形在小正方形EFGH内,由于三角形ABC的面积不大于小正方形面积EFGH的![]() ,又EFGH的面积为
,又EFGH的面积为![]() ×
×![]() =
=![]() ;故三角形ABC的面积不大于
;故三角形ABC的面积不大于![]() ;
;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】先判断下面的图形是长方体还是正方体,再计算它们的表面积及体积。
长 | 宽 | 高 | 形状 | 表面积 | 体积 |
8cm | 6cm | 5cm | (_____) | (_____) | (_____) |
12dm | 9dm | 9dm | (_____) | (_____) | (_____) |
8m | 8m | 8m | (_____) | (_____) | (_____) |