题目内容
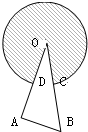 在图中,O是圆心,OD=4,C是OB的中点.阴影部分的面积是14π,求直角三角形OAB的面积.
在图中,O是圆心,OD=4,C是OB的中点.阴影部分的面积是14π,求直角三角形OAB的面积.
解:S扇形DOC=16π-14π=2π,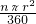 =2π,所以n=45°.
=2π,所以n=45°.
连接AC,则AC⊥OB,因为∠AOB=45°,所以∠OAC=45°,因此OC=AC=4.
又C是OB的中点,所以OB=8,则三角形OAB的面积为8×4÷2=16.
答:直角三角形OAB的面积是16.
分析:因为OD=4,所以圆的面积为16π.扇形DOC的面积是16π-14π=2π,根据扇形面积公式求得DOC即∠AOB=45°,
又因为∠A为直角,所以∠B=45°.连接AC,则AC⊥OB,因为∠AOB=45°,所以∠OAC=45°,因此OC=AC=4.
又C是OB的中点,所以OB=8,则三角形OAB的面积为8×4÷2.
点评:此题考查了圆、扇形以及三角形的面积,本题设计精彩,融合了多方面的知识.
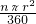 =2π,所以n=45°.
=2π,所以n=45°.连接AC,则AC⊥OB,因为∠AOB=45°,所以∠OAC=45°,因此OC=AC=4.
又C是OB的中点,所以OB=8,则三角形OAB的面积为8×4÷2=16.
答:直角三角形OAB的面积是16.
分析:因为OD=4,所以圆的面积为16π.扇形DOC的面积是16π-14π=2π,根据扇形面积公式求得DOC即∠AOB=45°,
又因为∠A为直角,所以∠B=45°.连接AC,则AC⊥OB,因为∠AOB=45°,所以∠OAC=45°,因此OC=AC=4.
又C是OB的中点,所以OB=8,则三角形OAB的面积为8×4÷2.

点评:此题考查了圆、扇形以及三角形的面积,本题设计精彩,融合了多方面的知识.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目

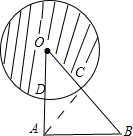
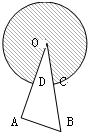 在图中,O是圆心,OD=4,C是OB的中点.阴影部分的面积是14π,求直角三角形OAB的面积.
在图中,O是圆心,OD=4,C是OB的中点.阴影部分的面积是14π,求直角三角形OAB的面积.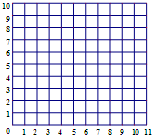 在图中先找出圆心O(5,3)的位置,再画半径长度是三格的圆,并画出圆互相垂直的一条半径和一条直径.
在图中先找出圆心O(5,3)的位置,再画半径长度是三格的圆,并画出圆互相垂直的一条半径和一条直径. 在图中,点O是
在图中,点O是