题目内容
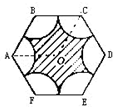 如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.
如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.分析:由图意可知:所要求的阴影面积是用正六边形的面积减去六个小扇形面积,正六边形的面积已知,现在关键是求小扇形的面积,由扇形面积公式S扇=
可求得,为此需要知道半径和扇形弧的度数,由已知正六边形每边所对圆心角为60°,那么∠AOC=120°,又知四边形ABCD是平行四边形,所以∠ABC=120°,这样就能求出扇形的面积.从而可以求得阴影部分的面积.
| nπR2 |
| 360 |
解答:解:如图所示,因为正六边形每边所对圆心角为60°,
那么∠AOC=120°,
又知四边形ABCD是平行四边形,所以∠ABC=120°,
则:阴影部分的面积=1040-6×
,
=1040-6×
,
=1040-2×314,
=1040-628,
=412(平方厘米);
答:阴影部分的面积是412平方厘米.
那么∠AOC=120°,
又知四边形ABCD是平行四边形,所以∠ABC=120°,
则:阴影部分的面积=1040-6×
| 3.14×102×120 |
| 360 |
=1040-6×
| 3.14×100 |
| 3 |
=1040-2×314,
=1040-628,
=412(平方厘米);
答:阴影部分的面积是412平方厘米.
点评:解答此题的关键是明白:阴影面积是用正六边形的面积减去六个小扇形面积.

练习册系列答案
相关题目

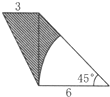
 将长12厘米,宽9厘米的长方形的长二等分,宽三等分,长方形内任意一点与分点或顶点连接,如图所示.求阴影部分的面积.
将长12厘米,宽9厘米的长方形的长二等分,宽三等分,长方形内任意一点与分点或顶点连接,如图所示.求阴影部分的面积.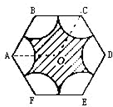 如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.
如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.