题目内容
（2012?东莞）自学下面这段材料，然后回答问题．
我们知道，在整数中“两个数的和等于这两个数的积”的情形不多，如2+2=2×2．但是在分数中，这种现象却很普遍．请观察下面的几个例子：
因为：
+
=4
×
=4
，所以
+
=
×
．
因为：
+
=4
×
=4
，所以
+
=
×
．
根据以上结果，我们发现了这样一个规律，两个分数，如果
例如
+
=
×
．
我们知道，在整数中“两个数的和等于这两个数的积”的情形不多，如2+2=2×2．但是在分数中，这种现象却很普遍．请观察下面的几个例子：
因为：
| 7 |
| 4 |
| 7 |
| 3 |
| 1 |
| 12 |
| 7 |
| 4 |
| 7 |
| 3 |
| 1 |
| 12 |
| 7 |
| 4 |
| 7 |
| 3 |
| 7 |
| 4 |
| 7 |
| 3 |
因为：
| 9 |
| 5 |
| 9 |
| 4 |
| 1 |
| 20 |
| 9 |
| 5 |
| 9 |
| 4 |
| 1 |
| 20 |
| 9 |
| 5 |
| 9 |
| 4 |
| 9 |
| 5 |
| 9 |
| 4 |
根据以上结果，我们发现了这样一个规律，两个分数，如果
分子
分子
相同，并且两个分母的和等于分子
两个分母的和等于分子
，那么这两个数的和等于它们的积．例如
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 3 |
分析：（1）根据所给例子，我们发现了这样一个规律，两个分数，分子相同，并且两个分数的分母的和等于分子，两个分数的和等于它们的积．
（2）根据找出的规律，写出符合规律的算式即可．
（2）根据找出的规律，写出符合规律的算式即可．
解答：解：（1）根据以上结果，我们发现了这样一个规律，两个分数，如果 分子相同，并且 两个分母的和等于分子，那么这两个分数的和等于它们的积．
（2）根据规律写出算式为：
+
=
×
．
故答案为：分子；两个分母的和等于分子；
；
；
；
．
（2）根据规律写出算式为：
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
故答案为：分子；两个分母的和等于分子；
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
点评：解决本题的关键是根据所给例子，我们发现了这样一个规律，两个分数，分子相同，并且两个分数的分母的和等于分子，两个数的和等于它们的积，再利用规律写算式即可．
练习册系列答案
名校课堂系列答案
相关题目
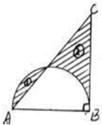（2012?东莞）如图：阴影2比阴影1面积大2.75平方厘米，圆的半径5厘米；求BC的长．