Question

（2013?北京模拟）如图，有一个长方形ABCD，其中BC=3BE，AE与BD相交于F，如果三角形EBF的面积为1，那么长方形ABCD的面积为

18

．

Answer 1

分析：如图所示，连接CF，则三角形BEF和三角形BFC，三角形BFC和三角形FDC都是等高不等底的三角形，则它们的面积比就等于对应底的比，又因三角形BEF的面积是1，则可以求出三角形BFC的面积，进而得出三角形FDC的面积，最后求出长方形的面积．

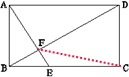
解答：解：如上图所示：因为BC=3BE，
则三角形BFC的面积是三角形BEF的面积的3倍，
则三角形BFC的面积是3，
三角形FDC是三角形BFC的面积的3倍，
则三角形FDC的面积是3×3=9，
所以三角形BDC的面积就是3+9=12，
因此长方形的面积是12×2=24；
故答案为：24．

点评：解答此题的主要依据是：等底不等高的三角形的面积比，就等于其对应底的比．