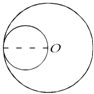
题目内容
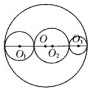 如图,O是大圆的圆心,O1,O2,O3分别是大圆内部三个小圆的圆心.那么大圆周长
如图,O是大圆的圆心,O1,O2,O3分别是大圆内部三个小圆的圆心.那么大圆周长=
=
小圆周长(添>、<或=)
分析:设圆O1,圆O2,圆O3分别是d1、d2、d3,则大圆的直径就是d1+d2+d3,由此利用圆的周长公式分别求出三个小圆的周长之和,与大圆的周长相比较即可解答.
解答:解:设圆O1,圆O2,圆O3分别是d1、d2、d3,则大圆的直径就是d1+d2+d3,
则三个小圆的周长之和是:πd1+πd2+πd3,
大圆的周长是:π(d1+d2+d3)=πd1+πd2+πd3,
所以大圆的周长等于小圆的周长之和.
故答案为:=.
则三个小圆的周长之和是:πd1+πd2+πd3,
大圆的周长是:π(d1+d2+d3)=πd1+πd2+πd3,
所以大圆的周长等于小圆的周长之和.
故答案为:=.
点评:此题考查了圆的周长的计算,可直接利用公式C=πd解答,同时此题也求证了一个结论:当大圆的直径是几个内接小圆的直径和时,大圆的周长就等于这几个小圆周长的和.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
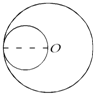 如图中,O是大圆的圆心,小圆的周长是大圆的几分之几?( )
如图中,O是大圆的圆心,小圆的周长是大圆的几分之几?( )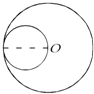 如图中,O是大圆的圆心,小圆的周长是大圆的几分之几?
如图中,O是大圆的圆心,小圆的周长是大圆的几分之几?


 如图,O是大圆的圆心,O1,O2,O3分别是大圆内部三个小圆的圆心.那么大圆周长________小圆周长
如图,O是大圆的圆心,O1,O2,O3分别是大圆内部三个小圆的圆心.那么大圆周长________小圆周长