题目内容
 把大正三角形每边八等份,组成如右图所示的三角形网.如果每个小三角形的面积都是1,求图中粗线所围成的三角形的面积.
把大正三角形每边八等份,组成如右图所示的三角形网.如果每个小三角形的面积都是1,求图中粗线所围成的三角形的面积.分析:根据皮克定理,设图形内的点为V,图形边上的点为L,则面积为L÷2-1+V.注意每个小三角形的面积都是1,则小平行四边形的面积为2.则面积为2(L÷2-1+V).
解答:解:①内部格点数为:12个;
②周界上格点数为:4个;
③阴影部分的面积是:2×(4÷2+12-1)=26(平方厘米).
答:图中粗线所围成的三角形的面积为26平方厘米.
②周界上格点数为:4个;
③阴影部分的面积是:2×(4÷2+12-1)=26(平方厘米).
答:图中粗线所围成的三角形的面积为26平方厘米.
点评:考查了格点图形的面积计算,熟记格点图形中的皮克定理是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目

 用花、白两种正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用花瓷砖(如图示).
用花、白两种正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用花瓷砖(如图示). 如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于
如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于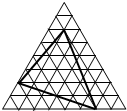 把大正三角形每边八等份,组成如右图所示的三角形网.如果每个小三角形的面积都是1,求图中粗线所围成的三角形的面积.
把大正三角形每边八等份,组成如右图所示的三角形网.如果每个小三角形的面积都是1,求图中粗线所围成的三角形的面积.