题目内容
 如图,长方体ABCD的面积为35平方厘米,左边三角形ABQ的面积是5平方厘米,右上边三角形APD的面积是7平方厘米,那么中间三角形AQP的面积是多少平方厘米?
如图,长方体ABCD的面积为35平方厘米,左边三角形ABQ的面积是5平方厘米,右上边三角形APD的面积是7平方厘米,那么中间三角形AQP的面积是多少平方厘米?分析:由图意可知:S△APQ=S长方形ABCD-S△ABQ-S△APD-S△PQC,S长方形ABCD、S△ABQ和S△APD已知,因此只要求出S△PQC即可,而求S△PQC,则应求出PC和QC与长方形的长和宽的关系,长方形的面积是已知的,于是可以依据长方形的面积,求出S△PQC,问题即可得解.
解答:解:因为S△ABQ=AB×BQ×
=5;
则AB×BQ=10,BQ=
;
QC=BC-
,
S△APD=AD×PD×
=7;
则AD×PD=14,PD=
,PC=DC-
,
所以S△PQC=
×(BC-
)×(DC-
)
=
×(AD-
)×(DC-
)
=
×(AD×DC-14-10+
)
=
×(35-14-10+
)
=
×(11+4)
=
×15
=7.5(平方厘米);
S△AQP=35-5-7-7.5
=30-14.5
=15.5(平方厘米);
答:中间三角形AQP的面积是15.5平方厘米.
| 1 |
| 2 |
则AB×BQ=10,BQ=
| 10 |
| AB |
QC=BC-
| 10 |
| AB |
S△APD=AD×PD×
| 1 |
| 2 |
则AD×PD=14,PD=
| 14 |
| AD |
| 14 |
| AD |
所以S△PQC=
| 1 |
| 2 |
| 10 |
| AB |
| 14 |
| AD |
=
| 1 |
| 2 |
| 10 |
| DC |
| 14 |
| AD |
=
| 1 |
| 2 |
| 140 |
| DC×AD |
=
| 1 |
| 2 |
| 140 |
| 35 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=7.5(平方厘米);
S△AQP=35-5-7-7.5
=30-14.5
=15.5(平方厘米);
答:中间三角形AQP的面积是15.5平方厘米.
点评:解答此题的关键是求出三角形PQC的面积,而求出PC和QC与长方形的长和宽的关系,更是关键的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
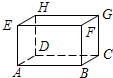 如图在长方体ABCD-EFGH中,与棱EF垂直的棱是
如图在长方体ABCD-EFGH中,与棱EF垂直的棱是 如图,长方体ABCD-A1B1C1D1中,与平面ADD1A1平行的棱是
如图,长方体ABCD-A1B1C1D1中,与平面ADD1A1平行的棱是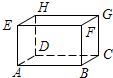 如图在长方体ABCD-EFGH中,与棱EF垂直的棱是________.(写出符合题意的所有棱)
如图在长方体ABCD-EFGH中,与棱EF垂直的棱是________.(写出符合题意的所有棱) 如图,长方体ABCD-A1B1C1D1中,与平面ADD1A1平行的棱是________.
如图,长方体ABCD-A1B1C1D1中,与平面ADD1A1平行的棱是________.