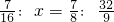题目内容
解方程
|
x×
|
x+
|
分析:(1)依据等式的性质,方程两边同时加
x,再同时减
,最后同时除以
求解,
(2)先化简方程,再依据等式的性质,方程两边同时除以
求解,
(3)先化简方程,再依据等式的性质,方程两边同时除以
求解.
| 3 |
| 4 |
| 1 |
| 8 |
| 3 |
| 4 |
(2)先化简方程,再依据等式的性质,方程两边同时除以
| 13 |
| 16 |
(3)先化简方程,再依据等式的性质,方程两边同时除以
| 5 |
| 4 |
解答:解:(1)
-
x=
,
-
x+
x=
+
x,
-
=
x+
-
,
=
x,
÷
=
x÷
,
x=
;
(2)x×
×
=52,
x=52,
x÷
=52÷
,
x=64;
(3)x+
x=25,
x=25,
x÷
=25÷
,
x=20.
| 3 |
| 8 |
| 3 |
| 4 |
| 1 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 1 |
| 8 |
| 3 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
x=
| 1 |
| 3 |
(2)x×
| 7 |
| 8 |
| 13 |
| 14 |
| 13 |
| 16 |
| 13 |
| 16 |
| 13 |
| 16 |
| 13 |
| 16 |
x=64;
(3)x+
| 1 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
x=20.
点评:等式的性质是解方程的依据,解方程时注意(1)方程能化简先化简,(2)等号要对齐.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目