题目内容
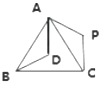
【题目】如下图,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是________;(2)旋转角度是________(3)△ADP是________三角形.
【答案】A 60° 正三角形
【解析】
旋转中固定不变的点就是旋转中心;
根据正三角形内角和确定旋转度数;
然后正三角形的特征判断三角形ADP的形状即可.
三角形ABD和三角形ACP有共同点A,所以是绕A点旋转,故旋转中心是A;
线段AB旋转后是AC,而三角形ABC是正三角形,所以AB到AC旋转了60°;
在三角形ADP中AP是AD旋转后的对应线段,所以想等,∠BAD旋转后是∠CAP,所以两角相等,因此,∠DAP=60°,故三角形ACP是正三角形.
故答案为:A、60°;正三角形

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
