题目内容
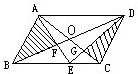 如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是________.
如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是________.
1:3
分析:由题意可知:因为O是AC、BD的中点,所以S△AOB=S△BOC=S△COD=S△ADO= S?ABCD=
S?ABCD= ×8×3=6平方厘米,S△BEF+S△CGE=S△BOC-S四边形EFOG=6-2=4平方厘米,S阴影=
×8×3=6平方厘米,S△BEF+S△CGE=S△BOC-S四边形EFOG=6-2=4平方厘米,S阴影= S?ABCD-(S△BEF+S△CGE)=12-4=8平方厘米,所以S阴影:S?ABCD=8:24=1:3;从而问题得解.
S?ABCD-(S△BEF+S△CGE)=12-4=8平方厘米,所以S阴影:S?ABCD=8:24=1:3;从而问题得解.
解答:因为O是AC、BD的中点,
所以S△AOB=S△BOC=S△COD=S△ADO,
= S?ABCD,
S?ABCD,
= ×8×3,
×8×3,
=6平方厘米,
S△BEF+S△CGE=S△BOC-S四边形EFOG,
=6-2=4(平方厘米),
S阴影= S?ABCD-(S△BEF+S△CGE),
S?ABCD-(S△BEF+S△CGE),
=12-4=8(平方厘米),
S阴影:S平ABCD=8:24=1:3;
答:阴影部分的面积与平行四边形的面积之比是1:3.
故答案为:1:3.
点评:解决此题的关键是利用等积转换,即等底等高的三角形面积相等,再结合阴影与平行四边形的关系,从而利用已知条件求得阴影部分的面积.
分析:由题意可知:因为O是AC、BD的中点,所以S△AOB=S△BOC=S△COD=S△ADO=
 S?ABCD=
S?ABCD= ×8×3=6平方厘米,S△BEF+S△CGE=S△BOC-S四边形EFOG=6-2=4平方厘米,S阴影=
×8×3=6平方厘米,S△BEF+S△CGE=S△BOC-S四边形EFOG=6-2=4平方厘米,S阴影= S?ABCD-(S△BEF+S△CGE)=12-4=8平方厘米,所以S阴影:S?ABCD=8:24=1:3;从而问题得解.
S?ABCD-(S△BEF+S△CGE)=12-4=8平方厘米,所以S阴影:S?ABCD=8:24=1:3;从而问题得解.解答:因为O是AC、BD的中点,
所以S△AOB=S△BOC=S△COD=S△ADO,
=
 S?ABCD,
S?ABCD,=
 ×8×3,
×8×3,=6平方厘米,
S△BEF+S△CGE=S△BOC-S四边形EFOG,
=6-2=4(平方厘米),
S阴影=
 S?ABCD-(S△BEF+S△CGE),
S?ABCD-(S△BEF+S△CGE),=12-4=8(平方厘米),
S阴影:S平ABCD=8:24=1:3;
答:阴影部分的面积与平行四边形的面积之比是1:3.
故答案为:1:3.
点评:解决此题的关键是利用等积转换,即等底等高的三角形面积相等,再结合阴影与平行四边形的关系,从而利用已知条件求得阴影部分的面积.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是
如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是 如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度.
如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度.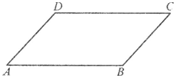 如图,平行四边形中相邻两边AB:AD=4:3,如果AD=4.5厘米,那么AB的长度是
如图,平行四边形中相邻两边AB:AD=4:3,如果AD=4.5厘米,那么AB的长度是 (2010?邯山区)已知如图,平行四边形ABCD的边AB是半圆O的直径,边AB 的中点O是半圆的圆心,且半圆O的圆周经过点D,DO与AB垂直,垂足是点O,AB=6.求图中阴影部分的面积.
(2010?邯山区)已知如图,平行四边形ABCD的边AB是半圆O的直径,边AB 的中点O是半圆的圆心,且半圆O的圆周经过点D,DO与AB垂直,垂足是点O,AB=6.求图中阴影部分的面积. (2013?华亭县模拟)如图,平行四边形相邻的两条边AB与BC的长度的比是
(2013?华亭县模拟)如图,平行四边形相邻的两条边AB与BC的长度的比是