题目内容
某公司在甲、乙两座仓库分别有农用车
12辆和6辆.现需要调往A县10辆,调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.问怎样调运,使总运费正好为900元.解:如图
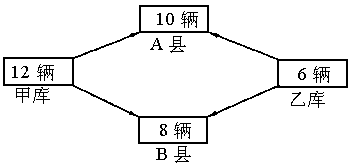
(1)
设从乙库调往A县x辆农用车,那么由乙库到A县的运费为________元.(2)
从乙库调往B县________辆农用车,其运费为________元.(3)
从甲库调往A县________辆农用车,其运费为________元.(4)
从甲库调往B县________辆农用车,其运费为________元.所以表示总运费的式子为:
____________________可列方程为:
__________________
答案:略
解析:
解析:
|
(1) 运费30x元;(2)(6 -x)辆,50(6-x)元;(3)(10 -x)辆,40(10-x)元;(4)[12 -(10-x)]辆,80[12-(10-x)]元总运费: 30x+50(6-x)+40(10-x)+80[12-(10-x)]方程: 30x+50(6-x)+40(10-x)+80[12-(10-x)]=900 |

练习册系列答案
相关题目