题目内容
 (2011?高县)有一根如图一样弯曲的绳子,想要在虚线之间用与虚线平行的方式剪切,把绳子分成几段,请回答问题:
(2011?高县)有一根如图一样弯曲的绳子,想要在虚线之间用与虚线平行的方式剪切,把绳子分成几段,请回答问题:(1)下面是剪切的情况,在括号里填上适当的数(绳子上面的虚线表示剪切的线)

(2)如果用●表示上面剪切的次数,○表示被分成的相应段数,请你用语音或算式表示●和○的关系.
(3)如果这样剪切15次,绳子被分成
46
46
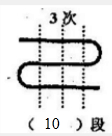
段.分析:(1)数出绳子的段数为10段,填入图下的括号;
(2)剪切1次绳子为4段,剪切2次绳子是7段,剪切3次绳子是10段…;
第一次是4段,然后每多剪切一次绳子的段数多3,段数与次数之间的关系是:○=4+(●-1)×3,然后化简即可;
(3)把●=15代入公式计算即可.
(2)剪切1次绳子为4段,剪切2次绳子是7段,剪切3次绳子是10段…;
第一次是4段,然后每多剪切一次绳子的段数多3,段数与次数之间的关系是:○=4+(●-1)×3,然后化简即可;
(3)把●=15代入公式计算即可.
解答:解:(1)如图:
(2)第一次是4段,然后每多剪切一次绳子的段数多3,所以
○=4+(●-1)×3,
=4+●×3-1×3,
=3●+1;
即○=3●+1;
(3)当剪切15次时,就是●=15,那么
○=3×15+1,
=45+1,
=46;
答:剪切15次,绳子被分成46段.
故答案为:46.

(2)第一次是4段,然后每多剪切一次绳子的段数多3,所以
○=4+(●-1)×3,
=4+●×3-1×3,
=3●+1;
即○=3●+1;
(3)当剪切15次时,就是●=15,那么
○=3×15+1,
=45+1,
=46;
答:剪切15次,绳子被分成46段.
故答案为:46.
点评:此题考查了图形的变化,通过观察找到规律,同时总结出规律,即用代数式表示.

练习册系列答案
相关题目