[题目]在如图中AB.AC的长度是15.BC的长度是9．把BC折过去与AC重合.B点落在E点上.求三角形ADE与三角形ABC面积之比．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在如图中AB，AC的长度是15，BC的长度是9．把BC折过去与AC重合，B点落在E点上，求三角形ADE与三角形ABC面积之比．

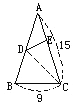
【答案】1：4

【解析】

试题分析：首先，根据△ADE和△DEC的高相等，那么可推出这两个三角形的面积之比，等于这两个三角形的底边之比为（15﹣9）：9=6：9=2：3．三角形BCD与三角形CDE面积相等．所以三角形ADE与三角形ABC的面积之比为2：8 即1：4

解：因为BC=CE=9，

所以AE=15﹣9=6（厘米）；

因为△ADE和△DEC的高相等，

所以△ADE和△DEC的面积比为（15﹣9）：9=6：9=2：3；

又因为三角形BCD与三角形CDE面积相等．

所以三角形ADE与三角形ABC的面积之比为2：8 即1：4．

答：三角形ADE与三角形ABC面积之比为1：4．

练习册系列答案

考必胜小学毕业升学考试试卷精选系列答案

（1）4天内，每部电影平均每天售票为________张、________张、________张、________张．(按顺序依次填写)

（2）照这样计算，这一周4部电影一共可能售票________张．

（3）如果每张票价是3元，这一周大约可收入________元票款．

（4）比较一下后4天，第________部电影观众最多，第________部观众最少，相差________人．

50分（______）5角 32＋33（______）89－22 3元（______）27角

（1）A站到B站相距　3　千米，B站到C站相距　　千米．

（2）返回时车速是每小时　　千米．

（3）电车往返的平均车速是每小时　　千米．

（______），70，75，（______），（______），90。

【题目】

（1）时针从12时起，绕点O顺时针旋转90°到（______）时

（2）时针从7时起，绕点O逆时针旋转90°到（______）时。

（3）时针从2时起，绕点O顺时针旋转90°到（______）时。

（4）时针从11时起，绕点O逆时针旋转90°到（______）时。

试题分类