题目内容
7. 为筹备迎春晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠上红色油纸,如图所示,已知圆筒高为108cm,其横截面周长为36cm,如果在表面缠上4圈油纸,最少应裁剪多长的油纸(油纸宽度忽略不计)
为筹备迎春晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠上红色油纸,如图所示,已知圆筒高为108cm,其横截面周长为36cm,如果在表面缠上4圈油纸,最少应裁剪多长的油纸(油纸宽度忽略不计)
分析 将圆柱沿一条母线展开,可得图形如下,只需求出每一圈所需的油纸的长度即可,展开后即转化为求解直角三角形的问题,在Rt△ABC中,AB已知,BC=$\frac{108}{4}$cm,根据勾股定理即得AC的长度,由于油纸缠绕4圈,故油纸的总长度为4AC的长度,据此解答即可.
解答 解:将圆筒展开后成为一个矩形,如图,整个油纸分成相等的4段,只需求出AC的长度即可,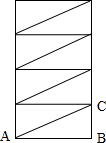
在Rt△ABC中,
因为AB=36cm,BC=$\frac{108}{4}$cm,
所以AC2=AB2+BC2=362+272=2025;
AC=45cm,
所以4AC=45×4=180(cm);
答:最少应裁剪180cm长的油纸.
点评 此题考查了平面展开-最短路径问题,此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径,一般情况是两点之间,线段最短,在平面图形上构造直角三角形即可解答问题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
15.直接写出得数.
| 1-0.95= | $\frac{2}{3}$-$\frac{1}{2}$= | 16×$\frac{5}{8}$= | 3.125+$\frac{1}{8}$= | 2-1$\frac{6}{7}$= |
| 1÷0.01= | 3.14×8= | 25×24= | $\frac{4}{5}$×$\frac{5}{9}$= | ($\frac{1}{3}$+$\frac{1}{5}$)×15= |
19.下面的3个图形都是由相同的小棒拼成,根据前3个图形的排列规律,第5个图形由( )根小棒拼成.


| A. | 20 | B. | 18 | C. | 16 | D. | 14 |