题目内容
4.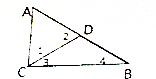 AC=AD,D是AB的中点,∠A=60°,∠1=60度,∠2=60度,∠3=30度,∠4=30度.
AC=AD,D是AB的中点,∠A=60°,∠1=60度,∠2=60度,∠3=30度,∠4=30度.
分析 首先根据AC=AD,∠A=60°,求出∠1、∠2的度数各是多少;然后判断出△ACD是等边三角形,推得CD=BD,再根据求出的∠2的度数,求出∠3、∠4的度数各是多少即可.
解答 解:因为AC=AD,
所以∠1=∠2=(180-60)÷2=120÷2=60(度),
所以△ACD是等边三角形,
所以CD=AD,
又因为D是AB的中点,
所以AD=BD,
所以BD=CD,
所以∠3=∠4=$\frac{1}{2}∠2=\frac{1}{2}×60=30$(度),
综上,可得
∠1=60度,∠2=60度,∠3=30度,∠4=30度.
故答案为:60、60、30、30.
点评 此题主要考查了三角形的内角和,以及等边三角形的性质和应用,要熟练掌握,解答此题的关键是判断出BD=CD.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
