题目内容
14.在横线内填入同一个数,使等式成立:(15×5-60)÷3=5;
$\frac{2175}{101}$÷25+4×$\frac{2175}{101}$=87.
分析 因为每个算式中横线上数都相等,可以设出这个数,把算式变成方程,然后根据解方程的方法求解.
解答 解:(1)设未知数是x,那么算式就是:
(15x-60)÷3=x
(15x-60)÷3×3=3x
15x-60=3x
15x-3x-60=3x-3x
12x-60+60=0+60
12x=60
12x÷12=60÷12
x=5
即:(15×5-60)÷3=5;
(2)设未知数是y,那么算式就是:
y÷25+4y=87
$\frac{1}{25}$y+4y=87
4$\frac{1}{25}$y=87
$\frac{101}{25}$y÷$\frac{101}{25}$=87÷$\frac{101}{25}$
y=$\frac{2175}{101}$
即:$\frac{2175}{101}$÷25+4×$\frac{2175}{101}$=87.
故答案为:5,5;$\frac{2175}{101}$,$\frac{2175}{101}$.
点评 解决本题无法直接根据算式各部分的关系进行求解,可以设出未知数,根据解方程的方法求解.

练习册系列答案
相关题目
4.甲把自己的钱的$\frac{1}{4}$给乙以后,甲、乙两人钱数相等,原来乙钱数占甲的( )
| A. | 50% | B. | 40% | C. | 200% | D. | 100% |
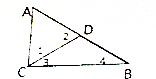 AC=AD,D是AB的中点,∠A=60°,∠1=60度,∠2=60度,∠3=30度,∠4=30度.
AC=AD,D是AB的中点,∠A=60°,∠1=60度,∠2=60度,∠3=30度,∠4=30度. 在图中,正方形的面积是9平方分米,这个圆的周长是188.4厘米,面积是2826平方厘米.
在图中,正方形的面积是9平方分米,这个圆的周长是188.4厘米,面积是2826平方厘米.