题目内容
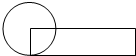如图，把一个半径4厘米的圆形纸片剪成一个近似的长方形，对于圆和长方形，它们的面积相等吗？周长相等吗？如果相等，则需回答“相等”就行了；如果不相等，则需计算出增加或减少了多少．
解：（1）因为，在剪与拼的过程中，纸片的面的大小没有发生变化，
所以，对于圆和长方形，它们的面积相等；
（2）因为拼成的长方形的周长比圆的周长增加了2个圆的半径，
所以增加的周长为：4×2=8（厘米），
答：拼成的长方形与圆的面积相等；拼成的长方形比圆的周长增加了8厘米．
分析：（1）根据“把一个半径4厘米的圆形纸片剪成一个近似的长方形”，知道在剪与拼的过程中，纸片的面的大小没有发生变化，所以对于圆和长方形，它们的面积相等；
（2）因为拼成的长方形的长是圆周长的一半，拼成的长方形的宽是圆的半径，所以拼成的长方形的周长比圆的周长增加了2个圆的半径，由此列式解决问题．
点评：解答此题的关键是，知道拼成的长方形与原来的圆的关系，即拼成的长方形的长等于圆周长的一半，拼成的长方形的宽等于圆的半径，由此解决问题．
所以，对于圆和长方形，它们的面积相等；
（2）因为拼成的长方形的周长比圆的周长增加了2个圆的半径，
所以增加的周长为：4×2=8（厘米），
答：拼成的长方形与圆的面积相等；拼成的长方形比圆的周长增加了8厘米．
分析：（1）根据“把一个半径4厘米的圆形纸片剪成一个近似的长方形”，知道在剪与拼的过程中，纸片的面的大小没有发生变化，所以对于圆和长方形，它们的面积相等；
（2）因为拼成的长方形的长是圆周长的一半，拼成的长方形的宽是圆的半径，所以拼成的长方形的周长比圆的周长增加了2个圆的半径，由此列式解决问题．
点评：解答此题的关键是，知道拼成的长方形与原来的圆的关系，即拼成的长方形的长等于圆周长的一半，拼成的长方形的宽等于圆的半径，由此解决问题．
练习册系列答案
相关题目
（2011?郑州模拟）如图是一张边长4厘米的正方形纸．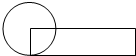
如图，把一个半径4厘米的圆形纸片剪成一个近似的长方形，对于圆和长方形，它们的面积相等吗？周长相等吗？如果相等，则需回答“相等”就行了；如果不相等，则需计算出增加或减少了多少．
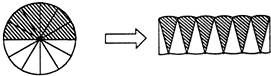（2010?泸西县模拟）如图把半径5厘米的圆形硬纸片剪开后，成一个近似的长方形，这个长方形的周长是