Question

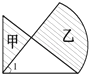
【题目】一个直角梯形的上底、下底和高分别是18，27，24厘米，且三角形ADE，ABF及四边形AECF面积相等，那么三角形AEF的面积是多少？

Answer 1

【答案】156平方厘米

【解析】

试题分析：三角形ABF、三角形ADE和四边形AECF把梯形平均分成了3部分，根据梯形的面积求出求出四边形AECF面积，再根据三角形ABF、三角形ADE的面积求出EC和CF的长度，进而求出三角形EFC的面积；用四边形AECF面积﹣三角形EFC的面积就是三角形AEF的面积．

解：大梯形的面积是：（18+27）×24÷2=540（平方厘米）

540÷3=180（平方厘米）

DE=180×2÷18=20（厘米），

EC=24﹣4=4（厘米），

BF=180×2÷24=15（厘米），

FC=12（厘米），

S△AEF=SAECF﹣S△ECF

=180﹣12×4÷2

=180﹣24，

=156（平方厘米）．

答：三角形AEF的面积是156平方厘米．