题目内容
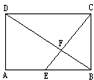 如图,E是长方形ABCD边AB的中点,已知三角形EBF的面积是1cm2,求长方形ABCD的面积.
如图,E是长方形ABCD边AB的中点,已知三角形EBF的面积是1cm2,求长方形ABCD的面积.分析:我们运用三角形的相似求出△BEF与△DCF的相似比,进一步求出S△DCF的面积,把各部分的面积加在一起,进一步求出长方形的面积.
解答:解:作图如下:
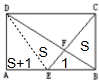
因为长方形ABCD,AB∥CD,AB=CD,BE=
AB=
CD,
所以△BEF∽△DCF,
S△BEF:SDCF=(
CD÷CD)2,
=
;
S△CDF=1÷
=4(平方厘米);
(S+1+S+S+1+4)÷4=S+1,
(3S+6)×
=S+1,
S+
=S+1,
S-
S+
-1=S-
S+1-1,
S=
,
S×4=
×4,
S=2;
长方形的面积是:S+1+S+S+1+4=2+1+2+2+1+4=12(平方厘米);
答:长方形ABCD的面积12平方厘米.

因为长方形ABCD,AB∥CD,AB=CD,BE=
| 1 |
| 2 |
| 1 |
| 2 |
所以△BEF∽△DCF,
S△BEF:SDCF=(
| 1 |
| 2 |
=
| 1 |
| 4 |
S△CDF=1÷
| 1 |
| 4 |
(S+1+S+S+1+4)÷4=S+1,
(3S+6)×
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
S=2;
长方形的面积是:S+1+S+S+1+4=2+1+2+2+1+4=12(平方厘米);
答:长方形ABCD的面积12平方厘米.
点评:本题运用三角形的相似,三角形的面积的比就是它们相似比的平方,进一步求出长方形的面积即可.

练习册系列答案
相关题目
 课外拓展
课外拓展 如图,是一个长方形ABCD,AB=20cm,BC=12cm,BC的三分之一处有一固定的点E,在C处有一个能移动的点P.点P以每秒4cm的速度向D点移动,求:
如图,是一个长方形ABCD,AB=20cm,BC=12cm,BC的三分之一处有一固定的点E,在C处有一个能移动的点P.点P以每秒4cm的速度向D点移动,求: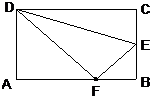 如图.长方形ABCD的长为6,宽为4,E是BC的中点.能否在线段AB上找一点F,使得△DEF的面积为13?若能,请说出F点的具体位置;若不能,请说明理由.
如图.长方形ABCD的长为6,宽为4,E是BC的中点.能否在线段AB上找一点F,使得△DEF的面积为13?若能,请说出F点的具体位置;若不能,请说明理由.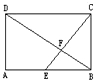 如图,E是长方形ABCD边AB的中点,已知三角形EBF的面积是1cm2,求长方形ABCD的面积.
如图,E是长方形ABCD边AB的中点,已知三角形EBF的面积是1cm2,求长方形ABCD的面积.