题目内容
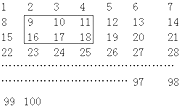 把从1到100的自然数如下表那样排列.在这个数表里面,把长的方面的三个数,宽的方面的二个数,一共六个数用长方形框围起来,六个数的和为81.在数表别的地方,如上述一样地围起来的六个数的和为429,那么长方形框子里的最大的数是________.
把从1到100的自然数如下表那样排列.在这个数表里面,把长的方面的三个数,宽的方面的二个数,一共六个数用长方形框围起来,六个数的和为81.在数表别的地方,如上述一样地围起来的六个数的和为429,那么长方形框子里的最大的数是________.
76
分析:观察已框出的六个数,10是上面一行的中间数,17是下面一行的中间数,10+17=27,是上、下两行中间数之和.这个中间数之和可以用(9+10+11+16+17+18)÷3=27求得.利用框中六个数的这种特点,求方框中的最大数.上、下两行中间数之和是429÷3=143,又知上一行的数比下一行对应的数小7,所以下一行的中间数是(143+7)÷2=75,最大数是75+1=76.
解答:数表中数的排列有个规律,中间的一个数是它前后两个数的平均数,相对的上、下两数的差是7,中间上、下两个数的和是429÷3=143,下面中间的那个数是(143+7)÷2=75,
所以框子里最大的数是75+1=76.
答:长方形框子里的最大的数是76.
故答案为:76.
点评:此题考查学生的观察与分析能力.对于这类题目应细细观察,找出特点或规律,再进行推算.
分析:观察已框出的六个数,10是上面一行的中间数,17是下面一行的中间数,10+17=27,是上、下两行中间数之和.这个中间数之和可以用(9+10+11+16+17+18)÷3=27求得.利用框中六个数的这种特点,求方框中的最大数.上、下两行中间数之和是429÷3=143,又知上一行的数比下一行对应的数小7,所以下一行的中间数是(143+7)÷2=75,最大数是75+1=76.
解答:数表中数的排列有个规律,中间的一个数是它前后两个数的平均数,相对的上、下两数的差是7,中间上、下两个数的和是429÷3=143,下面中间的那个数是(143+7)÷2=75,
所以框子里最大的数是75+1=76.
答:长方形框子里的最大的数是76.
故答案为:76.
点评:此题考查学生的观察与分析能力.对于这类题目应细细观察,找出特点或规律,再进行推算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 把从1到100的自然数如下表那样排列.在这个数表里面,把长的方面的三个数,宽的方面的二个数,一共六个数用长方形框围起来,六个数的和为81.在数表别的地方,如上述一样地围起来的六个数的和为429,那么长方形框子里的最大的数是
把从1到100的自然数如下表那样排列.在这个数表里面,把长的方面的三个数,宽的方面的二个数,一共六个数用长方形框围起来,六个数的和为81.在数表别的地方,如上述一样地围起来的六个数的和为429,那么长方形框子里的最大的数是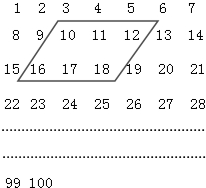 把从1到100的自然数如下表排列,在这个数表里,若用如图形状的图形去图数,这六个数的和为84,若用这个图形圈得的数的和为432,则圈得的最大数是多少?
把从1到100的自然数如下表排列,在这个数表里,若用如图形状的图形去图数,这六个数的和为84,若用这个图形圈得的数的和为432,则圈得的最大数是多少?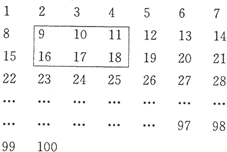 把从1到100的自然数如下表那样排列,在这个数表里,把长的方面的三个数,宽的方面的二个数,一共六个数用长方形框围起来,六个数的和为81,在数表别的地方,如上述一样地围起来的六个数的和为465,则长方形框子里的最大的数是
把从1到100的自然数如下表那样排列,在这个数表里,把长的方面的三个数,宽的方面的二个数,一共六个数用长方形框围起来,六个数的和为81,在数表别的地方,如上述一样地围起来的六个数的和为465,则长方形框子里的最大的数是 把从1到100的自然数如下表排列,在这个数表里,若用如图形状的图形去图数,这六个数的和为84,若用这个图形圈得的数的和为432,则圈得的最大数是多少?
把从1到100的自然数如下表排列,在这个数表里,若用如图形状的图形去图数,这六个数的和为84,若用这个图形圈得的数的和为432,则圈得的最大数是多少?