题目内容
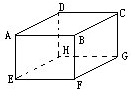
正方体上有8个顶点（如右图），上面分别标有8个连续的自然数．如果要使每一面4个顶点上的数之和为222，那么这8个连续自然数中最小的一个应该是52
52
．分析：假设这8个连续自然数中最小的一个是a，则其他七个数为a+1、a+2、a+3、a+4、a+5、a+6、a+7，由已知，每一面4个顶点上的数之和为222，6个面上数字总和为222×6，也正好是8个顶点的数字加了3遍，列式，求解．
解答：解：假设这8个连续自然数中最小的一个是a，由已知，得：
（8a+1+2+3+4+5+6+7）×3=222×6，
（8a+28）×3=222×6，
8a+28=222×2，
2a+7=111，
2a=104，
a=52；
答：那么这8个连续自然数中最小的一个应该是 52．
故答案为：52．
（8a+1+2+3+4+5+6+7）×3=222×6，
（8a+28）×3=222×6，
8a+28=222×2，
2a+7=111，
2a=104，
a=52；
答：那么这8个连续自然数中最小的一个应该是 52．
故答案为：52．
点评：此题此题考查了凑数谜，列出等式，凑数，即可得解．
练习册系列答案
步步高达标卷系列答案
相关题目
在正方体的8个顶点处分别标上1，2，3，4，5，6，7，8，然后再把每条棱两端所标的两个数之和写在这条棱的中点，问各棱中点所写的数是否可能恰有五种不同数值？各棱中点所写的数是否可能恰有四种不同数值？如果可能，对照如图在表中填上正确的数字；如果不可能，说明理由．