题目内容
 如图,l与m是两条平行直线,在直线l上有且只有4个不同的点,请你在m上取若干个不同的点,将直线l与m上的点连成线段,这些线段在l与m之间的交点最少有60个时,那么在直线m上至少要取
如图,l与m是两条平行直线,在直线l上有且只有4个不同的点,请你在m上取若干个不同的点,将直线l与m上的点连成线段,这些线段在l与m之间的交点最少有60个时,那么在直线m上至少要取5
5
个点.分析:设直线m上有x个点,l与m之间交点的个数由l上的两点与m上的两点唯一确定.在l上的四个点中选两点,有
=6(种)方法,在m的x个点中选两点,有
种方法.故其在l与m的交点个数为6×
≥60,据此解这个不等式即可求出x的取值范围,从而解决问题.
| 4×3 |
| 2 |
| x(x-1) |
| 2 |
| x(x-1) |
| 2 |
解答:解:设直线m上有x个点,l与m之间交点的个数由l上的两点与m上的两点唯一确定.
在l上的四个点中选两点,有
=6(种)方法,
在m的x个点中选两点,有
种方法.
故其在l与m的交点个数为6×
≥60,
即x(x-1)≥20,
解得x≥5.
所以在直线m上至少要取5个点.
答:在直线m上至少要取5个点.
故答案为:5.
在l上的四个点中选两点,有
| 4×3 |
| 2 |
在m的x个点中选两点,有
| x(x-1) |
| 2 |
故其在l与m的交点个数为6×
| x(x-1) |
| 2 |
即x(x-1)≥20,
解得x≥5.
所以在直线m上至少要取5个点.
答:在直线m上至少要取5个点.
故答案为:5.
点评:解答此题的关键是,根据题意,设出未知数,再根据所给出的信息,列出不定方程,解答即可.

练习册系列答案
相关题目
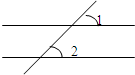 如图,a和b是两条互相平行的直线,∠1和∠2谁大?( )
如图,a和b是两条互相平行的直线,∠1和∠2谁大?( ) 如图,a、b是两条平行线,甲、乙两阴影部分的面积关系是( )
如图,a、b是两条平行线,甲、乙两阴影部分的面积关系是( )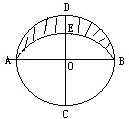 如图,AB与CD是两条垂直的直径,圆O的半径为15厘米,
如图,AB与CD是两条垂直的直径,圆O的半径为15厘米,
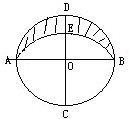 如图,AB与CD是两条垂直的直径,圆O的半径为15厘米,
如图,AB与CD是两条垂直的直径,圆O的半径为15厘米, 是以C为圆心,AC为半径的圆弧,求阴影部分的面积.
是以C为圆心,AC为半径的圆弧,求阴影部分的面积.