题目内容
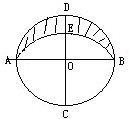 如图,AB与CD是两条垂直的直径,圆O的半径为15厘米,
如图,AB与CD是两条垂直的直径,圆O的半径为15厘米,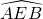 是以C为圆心,AC为半径的圆弧,求阴影部分的面积.
是以C为圆心,AC为半径的圆弧,求阴影部分的面积.
解:因为三角形ABC的面积为: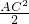 =
=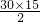 ,
,
所以AC2=30×15;
阴影部分的面积=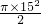 -(πAC2×
-(πAC2× -30×15×
-30×15× ),
),
=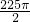 -(
-(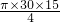 -
-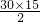 ),
),
=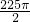 -(
-(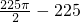 ),
),
=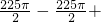 225,
225,
=225(平方厘米);
答:阴影部分的面积是225平方厘米.
分析:由图意可知:如图所示,连接AC、BC,则阴影部分的面积=半径为15厘米的圆面积的 -(半径为AC的
-(半径为AC的 圆的面积-三角形ABC的面积),又因AB=30厘米,OC=15厘米,从而可以依据三角形ABC的面积求出AC的长度,进而求得阴影部分的面积.
圆的面积-三角形ABC的面积),又因AB=30厘米,OC=15厘米,从而可以依据三角形ABC的面积求出AC的长度,进而求得阴影部分的面积.
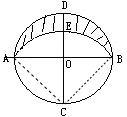
点评:解答此题的关键是:连接AC、BC,且阴影部分的面积=半径为15厘米的圆面积的 -(半径为AC的
-(半径为AC的 圆的面积-三角形ABC的面积).
圆的面积-三角形ABC的面积).
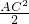 =
=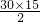 ,
,所以AC2=30×15;
阴影部分的面积=
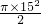 -(πAC2×
-(πAC2× -30×15×
-30×15× ),
),=
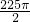 -(
-(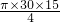 -
-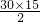 ),
),=
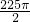 -(
-(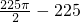 ),
),=
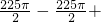 225,
225,=225(平方厘米);
答:阴影部分的面积是225平方厘米.
分析:由图意可知:如图所示,连接AC、BC,则阴影部分的面积=半径为15厘米的圆面积的
 -(半径为AC的
-(半径为AC的 圆的面积-三角形ABC的面积),又因AB=30厘米,OC=15厘米,从而可以依据三角形ABC的面积求出AC的长度,进而求得阴影部分的面积.
圆的面积-三角形ABC的面积),又因AB=30厘米,OC=15厘米,从而可以依据三角形ABC的面积求出AC的长度,进而求得阴影部分的面积.
点评:解答此题的关键是:连接AC、BC,且阴影部分的面积=半径为15厘米的圆面积的
 -(半径为AC的
-(半径为AC的 圆的面积-三角形ABC的面积).
圆的面积-三角形ABC的面积). 
练习册系列答案
相关题目
 如图,AB与CD平行,面积不相等的两个三角形是( )
如图,AB与CD平行,面积不相等的两个三角形是( ) 如图所示,E是AD边上的中点,CE把梯形分成甲、乙两个部分,面积比是10:7,上底AB与下底CD的长度比是
如图所示,E是AD边上的中点,CE把梯形分成甲、乙两个部分,面积比是10:7,上底AB与下底CD的长度比是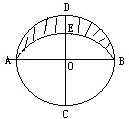 如图,AB与CD是两条垂直的直径,圆O的半径为15厘米,
如图,AB与CD是两条垂直的直径,圆O的半径为15厘米,
 如图梯形中的E是AD中点,线段CE把梯形分成甲、乙两个部分,面积比是10:7.那么梯形的上底AB与下底CD的长度比AB:CD=
如图梯形中的E是AD中点,线段CE把梯形分成甲、乙两个部分,面积比是10:7.那么梯形的上底AB与下底CD的长度比AB:CD=