题目内容
16.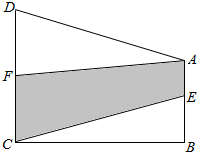 在四边形ABCD中,E为AB边上的中点,F为CD边上的中点,如果四边形AECF的面积是32cm2,求四边形ABCD的面积.
在四边形ABCD中,E为AB边上的中点,F为CD边上的中点,如果四边形AECF的面积是32cm2,求四边形ABCD的面积.
分析 如图,连结AC,根据E为AB边上的中点,F为CD边上的中点,可推出三角形ACE的面积=三角形BCE的面积,三角形ACF的面积=三角形ADF的面积,从而得出四边形ABCD的面积等于64平方厘米.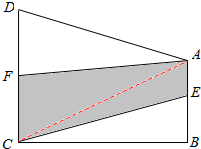
解答 解:连结AC,
因为E为AB边上的中点,F为CD边上的中点,
所以AE=EB,DF=FC,
所以S△ACE=S△BCE,
S△ACF=S△ADF,
所以S△ACE+S△ACF=S△BCE+S△ADF,
即四边形AECF的面积=S△BCE+S△ADF,
所以四边形ABCD的面积=四边形AECF的面积×2=32×2=64(平方厘米)
答:四边形ABCD的面积为64平方厘米.
点评 此题解答的关键在于通过作辅助线,推出三角形ACE的面积=三角形BCE的面积,三角形ACF的面积=三角形ADF的面积.

练习册系列答案
相关题目
5.朱家沟水库某天6:00开始蓄水,水库管理员每3小时观测一次水位上涨情况.下面是他的观测记录.
照这样的速度,要使水位上涨150厘米,一共要蓄水多少小时?
| 时间 | 9:00 | 12:00 | 15:00 | 18:00 |
| 与6:00比水位上涨/cm | 15 | 30 | 45 | 60 |

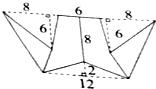 (1)如图是某工艺品的展开图,它的面积是多少?(单位:cm)
(1)如图是某工艺品的展开图,它的面积是多少?(单位:cm)