题目内容
18.(1)如图1,AB=2.0m,BD=1.5m,求AD的长;(2)如图2,AC=1.2m,BC=0.9m,求AB的长.
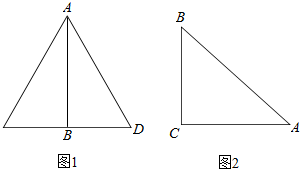
分析 (1)观察图形可知,三角形ABD是一个直角三角形,已知AB=2.0m,BD=1.5m,求AD,就是已知两条直角边,求斜边,依据勾股定理即可解答;
(2)观察图形可知,三角形ACB是一个直角三角形,已知AC=1.2m,BC=0.9m,求AB,也是已知两条直角边,求斜边,依据勾股定理即可解答.
解答 解:(1)在直角三角形ABD中,由勾股定理得:
AD=$\sqrt{{AB}^{2}{+BD}^{2}}$
=$\sqrt{{2.0}^{2}{+1.5}^{2}}$
=$\sqrt{6.25}$
=2.5(m);
答:AD的长是2.5m.
(2)在直角三角形ABC中,由勾股定理得:
AB=$\sqrt{{AC}^{2}{+BC}^{2}}$
=$\sqrt{{1.2}^{2}{+0.9}^{2}}$
=$\sqrt{2.25}$
=1.5(m);
答:AB的长是1.5m.
点评 本题考查了直角三角形中已知两条直角边求斜边的问题,关键是能熟练运用勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.如图是两个完全一样的平行四边形,涂色部分比较,( )
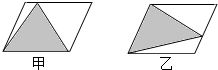
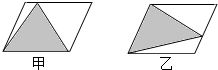
| A. | 甲面积大 | B. | 乙面积大 | C. | 面积相等 | D. | 无法比较 |
8.小明画了两条直线,这两条直线都和同一条直线垂直,这两条直线( )
| A. | 互相平行 | B. | 互相垂直 | C. | 相交 |