题目内容
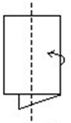 将一张正方形的纸如图按竖直中线对折,再将对折纸从它的竖直中线(用虚线表示)处剪开,得到三个矩形纸片:一个大的和两个小的,则一个小矩形的周长与大矩形的周长之比为________.
将一张正方形的纸如图按竖直中线对折,再将对折纸从它的竖直中线(用虚线表示)处剪开,得到三个矩形纸片:一个大的和两个小的,则一个小矩形的周长与大矩形的周长之比为________.
5:6
分析:根据题意,可设这个正方形的边长是a,由题意可得,对折一次后,正方形的边长变为原来边长的 ,即
,即 ,将对折纸从它的竖直中线(用虚线表示)处剪开,得到三个矩形纸片后,可以根据图可知,小矩形(矩形就是长方形)的宽是原来的
,将对折纸从它的竖直中线(用虚线表示)处剪开,得到三个矩形纸片后,可以根据图可知,小矩形(矩形就是长方形)的宽是原来的 =
= ,则大矩形的宽是小矩形的宽的2倍,即
,则大矩形的宽是小矩形的宽的2倍,即 ×2=
×2= a,一个大的和两个小的矩形的长数原来的正方形的边长,根据长方形的周长公式求出它们的周长,再根据比的意义就可求出一个小矩形的周长与大矩形的周长比.
a,一个大的和两个小的矩形的长数原来的正方形的边长,根据长方形的周长公式求出它们的周长,再根据比的意义就可求出一个小矩形的周长与大矩形的周长比.
解答:设正方形的边长是a.根据题意,小矩形的宽是:a× ×
× =
= a,长还是原来展开的边长,即a,
a,长还是原来展开的边长,即a,
则小矩形的周长是:(a+ a)×2=
a)×2= a;
a;
大矩形的宽是小矩形宽的2倍,可得大矩形的宽是: a×2=
a×2= a,长还是原来展开的边长,即a,
a,长还是原来展开的边长,即a,
则大矩形的周长是:(a+ a)×2=3a.
a)×2=3a.
一个小矩形的周长与大矩形的周长之比是: a:3a=
a:3a= :3=(
:3=( ):(3×2)=5:6.
):(3×2)=5:6.
故填:5:6.
点评:根据题意,先设出正方形的边长,由题意可以求出大小矩形的宽,再根据长方形的周长公式求出他们各自的周长,再根据比的意义既可以求出它们之间的周长比.
分析:根据题意,可设这个正方形的边长是a,由题意可得,对折一次后,正方形的边长变为原来边长的
 ,即
,即 ,将对折纸从它的竖直中线(用虚线表示)处剪开,得到三个矩形纸片后,可以根据图可知,小矩形(矩形就是长方形)的宽是原来的
,将对折纸从它的竖直中线(用虚线表示)处剪开,得到三个矩形纸片后,可以根据图可知,小矩形(矩形就是长方形)的宽是原来的 =
= ,则大矩形的宽是小矩形的宽的2倍,即
,则大矩形的宽是小矩形的宽的2倍,即 ×2=
×2= a,一个大的和两个小的矩形的长数原来的正方形的边长,根据长方形的周长公式求出它们的周长,再根据比的意义就可求出一个小矩形的周长与大矩形的周长比.
a,一个大的和两个小的矩形的长数原来的正方形的边长,根据长方形的周长公式求出它们的周长,再根据比的意义就可求出一个小矩形的周长与大矩形的周长比.解答:设正方形的边长是a.根据题意,小矩形的宽是:a×
 ×
× =
= a,长还是原来展开的边长,即a,
a,长还是原来展开的边长,即a,则小矩形的周长是:(a+
 a)×2=
a)×2= a;
a;大矩形的宽是小矩形宽的2倍,可得大矩形的宽是:
 a×2=
a×2= a,长还是原来展开的边长,即a,
a,长还是原来展开的边长,即a,则大矩形的周长是:(a+
 a)×2=3a.
a)×2=3a.一个小矩形的周长与大矩形的周长之比是:
 a:3a=
a:3a= :3=(
:3=( ):(3×2)=5:6.
):(3×2)=5:6.故填:5:6.
点评:根据题意,先设出正方形的边长,由题意可以求出大小矩形的宽,再根据长方形的周长公式求出他们各自的周长,再根据比的意义既可以求出它们之间的周长比.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 将一张正方形的纸如图按竖直中线对折,再将对折纸从它的竖直中线(用虚线表示)处剪开,得到三个矩形纸片:一个大的和两个小的,则一个小矩形的周长与大矩形的周长之比为
将一张正方形的纸如图按竖直中线对折,再将对折纸从它的竖直中线(用虚线表示)处剪开,得到三个矩形纸片:一个大的和两个小的,则一个小矩形的周长与大矩形的周长之比为 将一张正方形的纸进行折叠,然后如图所示,在完成折叠的最后一个步骤之后,用剪刀剪下所折成图形的一角,如果将纸打开,所得到的正方形将会与哪一个选项相类似呢?( )
将一张正方形的纸进行折叠,然后如图所示,在完成折叠的最后一个步骤之后,用剪刀剪下所折成图形的一角,如果将纸打开,所得到的正方形将会与哪一个选项相类似呢?( ) 将一张正方形的纸如图按竖直中线对折,再将对折纸从虚线处剪开,于是得到三个长方形纸片 一个大的两个小的,则每个小长方形周长与大长方形周长之比是( )
将一张正方形的纸如图按竖直中线对折,再将对折纸从虚线处剪开,于是得到三个长方形纸片 一个大的两个小的,则每个小长方形周长与大长方形周长之比是( ) 将一张正方形的纸如图按竖直中线对折,再将对折纸从虚线处剪开,于是得到三个长方形纸片 一个大的两个小的,则每个小长方形周长与大长方形周长之比是
将一张正方形的纸如图按竖直中线对折,再将对折纸从虚线处剪开,于是得到三个长方形纸片 一个大的两个小的,则每个小长方形周长与大长方形周长之比是


