题目内容
同样长的铁丝围成的圆、正方形、长方形中,________的面积最大.
圆
分析:三个图形的周长相同,而周长一定时,正方形的面积大于长方形的面积,由此设出周长比较出正方形与圆的面积大小即可.
解答:设它们的周长一定为L,
(1)因为周长一定时,所有的长方形中,正方形的面积最大,正方形是: ×
× =
= ;
;
(2)2πr=L,r=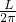 ,所以圆的面积是:π?r2=
,所以圆的面积是:π?r2=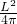 ;
;
 <
<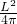 .所以周长一定时,正方形的面积小于圆的面积.
.所以周长一定时,正方形的面积小于圆的面积.
答:圆的面积最大.
故答案为:圆.
点评:抓住周长一定时,正方形的面积大于长方形的面积这一特点以及正方形和圆的面积公式即可解答此题.
分析:三个图形的周长相同,而周长一定时,正方形的面积大于长方形的面积,由此设出周长比较出正方形与圆的面积大小即可.
解答:设它们的周长一定为L,
(1)因为周长一定时,所有的长方形中,正方形的面积最大,正方形是:
 ×
× =
= ;
;(2)2πr=L,r=
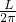 ,所以圆的面积是:π?r2=
,所以圆的面积是:π?r2=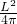 ;
; <
<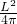 .所以周长一定时,正方形的面积小于圆的面积.
.所以周长一定时,正方形的面积小于圆的面积.答:圆的面积最大.
故答案为:圆.
点评:抓住周长一定时,正方形的面积大于长方形的面积这一特点以及正方形和圆的面积公式即可解答此题.

练习册系列答案
相关题目