题目内容
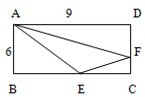三角形ABE，四边形AECF，三角形AFD的面积相等．求三角形AEF的面积．（单位：米）
解：三角形ABE，四边形AECF，三角形AFD的面积：6×9÷3=18（平方米），
BE的长度：18×2÷6=6（米），
DF的长度：18×2÷9=4（米），
三角形EFC的面积：（9-6）×（6-4）÷2，
=3×2÷2，
=3（平方米），
三角形AEF的面积：18-3=15（平方米），
答：三角形AEF的面积是15平方米．
分析：根据长方形的面积公式S=ab，求出长方形ABCD的面积，再除以3就是三角形ABE，四边形AECF，三角形AFD的面积，再求出BE与DF的长度，进而求出EC与CF的长度，继而求出三角形EFC的面积，最后求出三角形AEF的面积．
点评：本题主要是灵活利用三角形的面积公式求出三角形EFC的面积，进而求出三角形AEF的面积．
BE的长度：18×2÷6=6（米），
DF的长度：18×2÷9=4（米），
三角形EFC的面积：（9-6）×（6-4）÷2，
=3×2÷2，
=3（平方米），
三角形AEF的面积：18-3=15（平方米），
答：三角形AEF的面积是15平方米．
分析：根据长方形的面积公式S=ab，求出长方形ABCD的面积，再除以3就是三角形ABE，四边形AECF，三角形AFD的面积，再求出BE与DF的长度，进而求出EC与CF的长度，继而求出三角形EFC的面积，最后求出三角形AEF的面积．
点评：本题主要是灵活利用三角形的面积公式求出三角形EFC的面积，进而求出三角形AEF的面积．
练习册系列答案
快乐5加2金卷系列答案
相关题目
三角形ABE，四边形AECF，三角形AFD的面积相等．求三角形AEF的面积．（单位：米）
如图ABCD是一个平行四边形，CE的长度是BE的2倍，F是DC的中点，三角形ABE的面积是9平方厘米，那么三角形ADF的面积是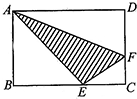
如图，三角形ADF与三角形ABE、四边形AFCE的面积相等，BC=9厘米，CD=6厘米，求阴影部分的面积（ ）
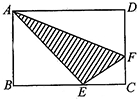如图，三角形ADF与三角形ABE、四边形AFCE的面积相等，BC=9厘米，CD=6厘米，求阴影部分的面积