题目内容
2.正方形ABCD中,已知CD=3FC,BC=3EC,问四边形ABGD与正方形ABCD的面积比是多少?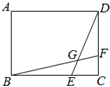
分析 首先根据CD=3FC,BC=3EC,判断出S△BGE=2S△CGE,S△DFG=2S△CFG;然后根据三角形面积和底的正比关系,求出四边形CFGE的面积占正方形ABCD的面积的几分之几,进而求出四边形ABGD的面积与正方形ABCD的面积比是多少即可.
解答 解:如图, ,
,
因为CD=3FC,BC=3EC,
所以S△BCF=S△DCE=$\frac{1}{6}$S正方形ABCD,
所以S△BGE=2S△CGE,S△DFG=2S△CFG,
所以S△CGE=${\frac{1}{4}S}_{△BCF}$,S△CFG=${\frac{1}{4}S}_{△DCE}$,
因此S四边形CEFG=${\frac{1}{2}S}_{△BCF}$=$\frac{1}{12}$S正方形ABCD,
因此S四边形ABGD=(1-$\frac{1}{6}-\frac{1}{6}+\frac{1}{12}$)S正方形ABCD=$\frac{3}{4}$S正方形ABCD,
因此S四边形ABGD:S正方形ABCD=3:4.
答:四边形ABGD与正方形ABCD的面积比是3:4.
点评 此题主要考查了相似三角形的性质,要熟练掌握,解答此题的关键是要明确:(1)三角形的高相等时,三角形的面积和三角形的底成正比;(2)四边形CFGE的面积占正方形ABCD的面积的$\frac{1}{12}$.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.一个长5cm、宽3cm的长方形按3:1放大,得到的图形的面积是原来的( )倍.
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
11.高一定,圆柱的体积和底面的半径( )
| A. | 成正比例 | B. | 成反比例 | C. | 不成比例 |
14.在表格的空格里填上适当的数,使每列的3个数量都相等.
| 6dm | 450kg | 32cm2 | 3250mL | 180cm | |
| 用分数表示 | m | t | dm2 | L | m |
| 用小数表示 | m | t | dm2 | L | m |
 校园里有一块长方形空地,长为24m,宽为12m,在空地里植了一块草坪(阴影部分),草坪的面积为多少平方米.
校园里有一块长方形空地,长为24m,宽为12m,在空地里植了一块草坪(阴影部分),草坪的面积为多少平方米.