题目内容
3. 实践操作
实践操作(1)在方框内画一个周长是12.56厘米的圆,并标出圆心O
(2)在所画圆中画两条相互垂直的直径.
(3)依次连接这两条直径的四个端点,得到一个正方形.
(4)这个正方形的面积是8平方厘米.
分析 先根据圆的周长求出圆的半径,由半径画出我们所需的圆,然后画两条相互垂直的直径,最后依次连接这两条直径的四个端点,得到一个正方形,再根据圆的内接四边形和小三角形的关系求出正方形的面积来.
解答 解:由题意知,周长为12.56厘米的圆的半径为:
12.56÷π÷2,
=12.56÷3.14÷2,
=2(厘米);
半径为2厘米的圆如下图所示:
在圆中两条互相垂直的直径如下图所求: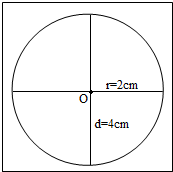
依次连接这两条直径的四个端点,得到一个正方形如下图所示:
可见,这个正方形是由四个小三角形组成的,且小三角形的面积两条直角边已知,
正方形的面积:4×(2×2÷2)=8(平方厘米),
答:这个正方形的面积是8平方厘米.
故答案为:8.
点评 此题考查了根据圆的周长求圆的半径,并考查了学生的作图能力,以及如何根据图求圆内接正方形的面积.

练习册系列答案
相关题目
18.直接写得数:
| 45+15×6= | 250÷5×8= | 6×5÷2×4= | 70+(100-10×5)= |
| 80-25= | (80÷20+80)÷4= | 360÷40= | 40×20= |
| 88÷22= | 160×5= |
15.用0、1、2、3中的两个数字可以组成( )个不同的两位数.
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
13.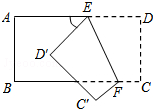 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′位置.若∠EFB=65°,则∠AED′等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′位置.若∠EFB=65°,则∠AED′等于( )
 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′位置.若∠EFB=65°,则∠AED′等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′位置.若∠EFB=65°,则∠AED′等于( )| A. | 70° | B. | 65° | C. | 50° | D. | 25° |
 如图中,涂色部分占整个图形的$\frac{(\;\;\;\;)}{(\;\;\;\;)}$,如果每个小长方形的面积是2平方分米,涂色部分的面积是3平方分米.
如图中,涂色部分占整个图形的$\frac{(\;\;\;\;)}{(\;\;\;\;)}$,如果每个小长方形的面积是2平方分米,涂色部分的面积是3平方分米.