题目内容
【题目】一辆汽车行驶的时间和所行的路程如下表。
时间（时） | 0 | 1 | 2 | 3 | 4 | 5 | … |
路程（千米） | 0 | 60 | 120 | … |
（1）把上表填写完整。
（2）时间和路程成正比例吗？
（3）根据上表描点，再顺次连接各点，你发现了什么？
【答案】（1）180、 240、 300.
（2）时间和路程成正比例.
（3）我发现时间和路程相交的点都在一条直线上，即正比例关系的图象是一条直线。
【解析】（1）60×3＝180（千米） 60×4＝240（千米） 60×5＝300（千米）;
（2）时间和路程是两种相关联的量，路程随着时间的变化而变化，路程÷时间＝速度（一定），所以时间和路程成正比例.
路程（千米） |
（3）
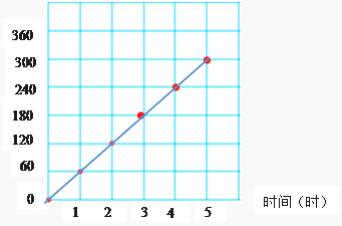我发现时间和路程相交的点都在一条直线上，即正比例关系的图象是一条直线。
金博士一点全通系列答案
【题目】下图的图象表示一幅地图图上距离与实际距离的关系.
图上距离（cm） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
实际距离（m） | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 |
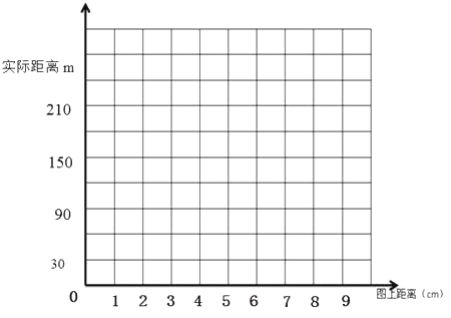
（1）图中的点A表示图上距离是1cm时，实际距离为30m.请你试着描出其他各点。
（2）图上距离与实际距离成________
（3）从图象可以看出这幅图的比例尺是________.
（4）当图上距离是12厘米时两地的实际距离是多少米？
【题目】一种花布的数量和总价如下表，看表回答问题。
数量∕米 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
总价∕元 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | … |
（1）分别写出各组总价和相对应的数量的比，求出比值。
（2）说明这个比值所表示的意义。
（3）表中的总价和数量成正比例吗？为什么？
（4）在下图中描出表示数量和对应总价的点，然后把它们连起来，说说图像的特点。
（5）利用图像回答，买2.5米花布要多少元？52元能买多少米花布？
【题目】红红打算到文具店买笔记本。
（1）购买同一种笔记本的数量和总价如下表。
数量(本) | 1 | 2 | 3 | 4 | 5 |
总价(元) | 5 | 10 | 15 | 20 | 25 |
①表中有哪两种量？它们是相关联的量吗？说明理由。
②写出这两种量中相对应的两个数的比，并求出比值。这些比值相等吗？
③这个比值表示的意义是什么？
④根据表中的数据，在下图中描点再依次连接。
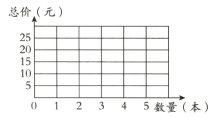
（2）红红没带那么多钱，她进行了一番比较统计，购买不同种类笔记本的单价和数量如下表。
单价(元/本) | 1 | 2 | 2.5 | |
数量(本) | 10 | 5 | 2 |
①把上表补充完整。
②表中( )和( )是两种相关联的量，( )随着( )的变化而变化。而且单价和数量的( )一定，也就是( )一定，所以单价和数量成( )比例。
（3）如果红红一定要买6本同样的笔记本，即数量一定，那么总价和单价成( )比例。
