题目内容
在一个盒子中有10个红球,8个绿球和一些黑球,每次从里面拿出一个球,结果拿出绿球的可能性小于 ,那么至少有 黑球.
,那么至少有 黑球.
- A.6
- B.7
- C.8
B
分析:假设摸出绿球的可能性等于 ,即盒子中球的总个数的
,即盒子中球的总个数的 是绿球的个数,根据已知一个数的几分之几是多少,求这个数,用除法求出盒子中球的总个数,然后减去盒子中红球和绿球的个数,即盒子中黑球个数;因为拿出绿球的可能性小于
是绿球的个数,根据已知一个数的几分之几是多少,求这个数,用除法求出盒子中球的总个数,然后减去盒子中红球和绿球的个数,即盒子中黑球个数;因为拿出绿球的可能性小于 所以用求出的黑球个数加1即可.
所以用求出的黑球个数加1即可.
解答:8÷ =24(个),
=24(个),
24-10-8+1,
=6+1,
=7(个);
答:至少有7个黑球.
故选:B.
点评:解答此题用到的知识点:先进行假设,进而根据已知一个数的几分之几是多少,求这个数,用除法求出盒子中球的总个数,然后求出当摸出绿球的可能性等于 时黑球的个数,然后加1即可.
时黑球的个数,然后加1即可.
分析:假设摸出绿球的可能性等于
 ,即盒子中球的总个数的
,即盒子中球的总个数的 是绿球的个数,根据已知一个数的几分之几是多少,求这个数,用除法求出盒子中球的总个数,然后减去盒子中红球和绿球的个数,即盒子中黑球个数;因为拿出绿球的可能性小于
是绿球的个数,根据已知一个数的几分之几是多少,求这个数,用除法求出盒子中球的总个数,然后减去盒子中红球和绿球的个数,即盒子中黑球个数;因为拿出绿球的可能性小于 所以用求出的黑球个数加1即可.
所以用求出的黑球个数加1即可.解答:8÷
 =24(个),
=24(个),24-10-8+1,
=6+1,
=7(个);
答:至少有7个黑球.
故选:B.
点评:解答此题用到的知识点:先进行假设,进而根据已知一个数的几分之几是多少,求这个数,用除法求出盒子中球的总个数,然后求出当摸出绿球的可能性等于
 时黑球的个数,然后加1即可.
时黑球的个数,然后加1即可. 
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
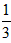 ,那么至少有黑球
,那么至少有黑球