题目内容
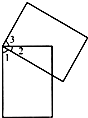如图，两个完全相同的长方形重叠了一部分，已知∠2=30°求：∠1+∠2+∠3．分析：由于两个重叠的图形是完全相同的长方形，根据长方形的特征，长方形的每个内角都是90°，因此可知：∠1+∠2=90°，∠2+∠3=90°，又因为已知∠2=30°，于是可以求出∠1和∠3的度数，代入∠1+∠2+∠3即可解决．
解答：解：因为长方形每个内角都是90°，
所以：∠1+∠2=90°，∠2+∠3=90°，
所以∠1=90°-∠2，
=90°-30°，
=60°；
∠3=90°-∠2，
=90°-30°，
=60°；
所以：∠1+∠2+∠3=60°+30°+60°=150°．
答：：∠1+∠2+∠3的度数是150°．
所以：∠1+∠2=90°，∠2+∠3=90°，
所以∠1=90°-∠2，
=90°-30°，
=60°；
∠3=90°-∠2，
=90°-30°，
=60°；
所以：∠1+∠2+∠3=60°+30°+60°=150°．
答：：∠1+∠2+∠3的度数是150°．
点评：本题考查了求几个角的度数的和，关键是根据图意找出所有角之间的关系．
练习册系列答案
相关题目
如图，两个完全相同的长方形中，阴影部分的面积（ ）
如图是两个完全相同的两个直角梯形重叠在一起，求阴影部分的面积．（单位：厘米）
如图，两个完全相同的圆相切，都与圆外边的正方形PQMN相切，共有5五个切点A、B、C、D、E，将1～9这九个数字分别放在这五个切点和正方形四个顶点上，使正方形每边上的三个数的和均为质数，则A、B、C、、D、E、M、N、Q、P对应的数分别为
如图，两个完全相同的正方形在两边的中点处部分重合．已知重合部分的面积是5平方厘米，阴影部分的面积是