题目内容
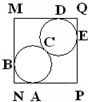 如图,两个完全相同的圆相切,都与圆外边的正方形PQMN相切,共有5五个切点A、B、C、D、E,将1~9这九个数字分别放在这五个切点和正方形四个顶点上,使正方形每边上的三个数的和均为质数,则A、B、C、、D、E、M、N、Q、P对应的数分别为
如图,两个完全相同的圆相切,都与圆外边的正方形PQMN相切,共有5五个切点A、B、C、D、E,将1~9这九个数字分别放在这五个切点和正方形四个顶点上,使正方形每边上的三个数的和均为质数,则A、B、C、、D、E、M、N、Q、P对应的数分别为4,9,5,2,1,6,8,3,7
4,9,5,2,1,6,8,3,7
.分析:因为6+2+3=11,3+1+7=11,8+4+7=19,6+9+8=23,11、19和23都是质数,满足正方形每边上的三个数的和均为质数;把5放在中间C处.由此得解.
解答:解:答案如图,
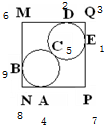
故答案为:4,9,5,2,1,6,8,3,7.

故答案为:4,9,5,2,1,6,8,3,7.
点评:此题考查了凑数谜以及质数与合数.质数是除了1和它本身外,没有约数的数,11、19、23、等等都是质数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,两个完全相同的长方形中,阴影部分的面积( )
如图,两个完全相同的长方形中,阴影部分的面积( )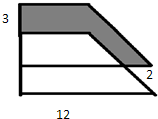 如图是两个完全相同的两个直角梯形重叠在一起,求阴影部分的面积.(单位:厘米)
如图是两个完全相同的两个直角梯形重叠在一起,求阴影部分的面积.(单位:厘米) 如图,两个完全相同的长方形重叠了一部分,已知∠2=30°求:∠1+∠2+∠3.
如图,两个完全相同的长方形重叠了一部分,已知∠2=30°求:∠1+∠2+∠3. 如图,两个完全相同的正方形在两边的中点处部分重合.已知重合部分的面积是5平方厘米,阴影部分的面积是
如图,两个完全相同的正方形在两边的中点处部分重合.已知重合部分的面积是5平方厘米,阴影部分的面积是