题目内容
【题目】在边长为20dm的正方形铁皮上剪圆片。
图1  图2
图2 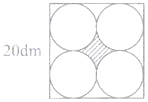
(1)如图1,正方形铁皮剪完一个圆后剩下的边角料的面积是多少?
(2)如图2,像这样剪4个大小相等的圆,剩下的边角料的面积是多少?正中心的边角料(阴影部分)面积是多少?
(3)猜想:继续像上面这样剪圆片,在正方形铁皮上剪下9个大小相等的圆,剩下的边角料是多少?剪16个圆呢?从中你发现了什么?为什么会这样呢?请写出你的想法。
【答案】(1)86dm2
(2)86dm2 21.5dm2
(3)86dm2 86dm2
从中我发现了剩下的边角料的面积是相等的,因为这些小圆的面积和都可以转化成图1的圆的面积,所以剩下的边角料面积不变
【解析】
(1)根据题意可知,要求边角料的面积,先求出正方形的面积,正方形的面积=边长×边长,然后求出圆的半径,圆的半径=正方形的边长÷2,再求出圆的面积,S=πr2,最后用正方形的面积-圆的面积=剩下的边角料的面积,据此列式解答;
(2)根据题意可知,要求边角料的面积,先求出正方形的面积,正方形的面积=边长×边长,然后求出小圆的半径,小圆的半径=正方形的边长÷4,再求出一个小圆的面积,S=πr2,然后用一个小圆的面积×4=4个小圆的面积之和,最后用正方形的面积-4个小圆的面积和=剩下的边角料的面积,据此列式解答;
要求正中心的边角料的面积,顺次连接4个小圆的圆心,可以得到一个边长10dm的正方形,然后用小正方形的面积-半径为5dm的圆的面积=正中心的边角料面积,据此列式解答;
(3)通过上面的计算,可以猜想:继续像上面这样剪圆片,在正方形铁皮上剪下9个大小相等的圆,剩下的边角料是86dm2;
剪16个圆,剩下的边角料是86dm2;
从中我发现了剩下的边角料的面积是相等的,因为这些小圆的面积和都可以转化成图1的圆的面积,所以剩下的边角料面积不变.
(1)正方形的面积:20×20=400(dm2);
圆的半径:20÷2=10(dm);
圆的面积:
3.14×102
=3.14×100
=314(dm2);
剩下的边角料面积:400-314=86(dm2).
答:正方形铁皮剪完一个圆后剩下的边角料的面积是86dm2.
(2)正方形的面积:20×20=400(dm2);
小圆的半径:20÷4=5(dm);
小圆的面积:
3.14×52
=3.14×25
=78.5(dm2)
四个小圆的面积之和:78.5×4=314(dm2)
剩下的边角料面积:400-314=86(dm2)
正中心的边角料面积:
10×10-3.14×52
=10×10-3.14×25
=100-78.5
=21.5(dm2)
答:正方形铁皮剪完一个圆后剩下的边角料的面积是86dm2;正中心的边角料面积是21.5dm2.
(3)猜想:继续像上面这样剪圆片,在正方形铁皮上剪下9个大小相等的圆,剩下的边角料是86dm2;剪16个圆,剩下的边角料是86dm2;从中我发现了剩下的边角料的面积是相等的,因为这些小圆的面积和都可以转化成图1的圆的面积,所以剩下的边角料面积不变