题目内容
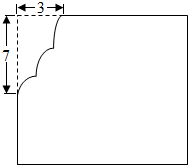 将一块边长为12cm的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮,则剪成的正方形铁皮的面积的最大值是( )
将一块边长为12cm的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮,则剪成的正方形铁皮的面积的最大值是( ) | cm | 2 |
分析:将一块边长为12厘米的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮,要考虑剪去的最少,还要求仍然是正方形,则有下列剪法是比较大的,其他剪法更小.分别求出三种情况下剪成的正方形铁皮的面积,比较大小,求出最大值,即可得解.
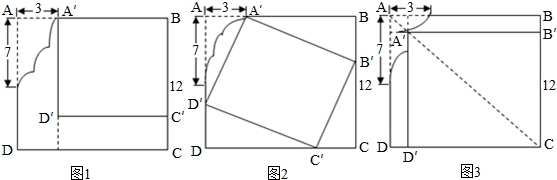
解答:解:如图1所示,使A′B=BC′=C′D′=D′A′=12-3=9(厘米),则正方形A′BC′D′的面积为9×9=8l(平方厘米).
如图2所示,使AA′=BB′=CC′=DD′=3(厘米),则正方形A′B′C′D′的面积为
12×12-4×
×3×(12-3)=90(平方厘米).
如图3所示,连接AC交曲线于点A′,使A′B′=B′C=CD′=D′A′.观察图3可知
A′B′=12-1.5=10.5(厘米).(注:A′B′的长度在(10.5士0.2)厘米之间均可.连接AC与缺损的边缘交与A'点,过A'分别作AB和AD的平行线A'B'和A'D',A'D'延长与AB交与一点H,A'H是缺损三角形的中位线,根据中位线的性质,同样平分另一边,因此AH的长是3除以2等于1.5,A'B'=BH=AB-AH=12-1.5=10.5,当然,这只是一个近似值)
于是正方形A′B′CD′的面积为10.5×10.5=110.25(平方厘米).
因为81<90<110.25,所以剪成的正方形铁皮的面积最大为110.25平方厘米.
答:剪成的正方形铁皮的面积最大为110.25平方厘米.
故选:B.
如图2所示,使AA′=BB′=CC′=DD′=3(厘米),则正方形A′B′C′D′的面积为
12×12-4×
| 1 |
| 2 |
如图3所示,连接AC交曲线于点A′,使A′B′=B′C=CD′=D′A′.观察图3可知
A′B′=12-1.5=10.5(厘米).(注:A′B′的长度在(10.5士0.2)厘米之间均可.连接AC与缺损的边缘交与A'点,过A'分别作AB和AD的平行线A'B'和A'D',A'D'延长与AB交与一点H,A'H是缺损三角形的中位线,根据中位线的性质,同样平分另一边,因此AH的长是3除以2等于1.5,A'B'=BH=AB-AH=12-1.5=10.5,当然,这只是一个近似值)
于是正方形A′B′CD′的面积为10.5×10.5=110.25(平方厘米).

因为81<90<110.25,所以剪成的正方形铁皮的面积最大为110.25平方厘米.
答:剪成的正方形铁皮的面积最大为110.25平方厘米.
故选:B.
点评:此题考查了最大和最小问题,剪成的正方形铁皮的面积最大,则材料的应用最节约.在生活实际中要求我们要多动脑筋.

练习册系列答案
相关题目
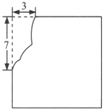 将一块边长为12cm的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮,则剪成的正方形铁皮的面积的最大值是
将一块边长为12cm的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮,则剪成的正方形铁皮的面积的最大值是 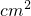 .
.