题目内容
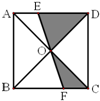如图，已知面积为1的正方形ABCD的对角线相交于点O，过点O任作一条直线分别交AD、BC于E、F，则阴影部分的面积是| 1 |
| 4 |
| 1 |
| 4 |
分析：下面阴影部分△OFC和△OEA关于0点中心对称，所以这两个三角形的面积相等，则阴影部分的面积就是△AOD的面积，两条对角线把正方形平均分成4份，其中的一份占
，即可得解．
| 1 |
| 4 |
解答：解：S△OFC=S△OEA，
S△OFC+S△ODE=S△AOD=
S正方形ABCD=
；
所以阴影部分的面积是
．
故答案为：
．
S△OFC+S△ODE=S△AOD=
| 1 |
| 4 |
| 1 |
| 4 |
所以阴影部分的面积是
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：发现△OFC和△OEA关于0点中心对称，是两个全等三角形是解决此题的关键．
练习册系列答案
相关题目
如图，已知最小圆的半径为1厘米，外面圆的半径依次大1厘米，直到第2008个圆，则阴影部分的面积为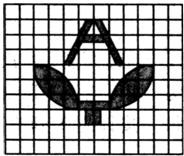
如图，已知每个小正方形的面积为1平方厘米，阴影部分的面积是
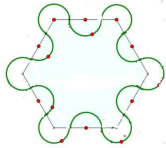小区花坛的平面图案如图，已知每条圆弧的半径都是1厘米，圆心分别组成正六边形的顶点和各边的中点，那么这个花坛的总面积是
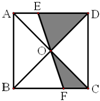如图，已知面积为1的正方形ABCD的对角线相交于点O，过点O任作一条直线分别交AD、BC于E、F，则阴影部分的面积是________．