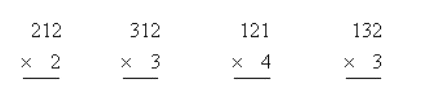题目内容
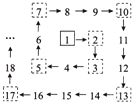
【题目】将自然数从1开始,顺次排成如图所示的螺旋形,其中2,3,5,7,…处为拐点,请问:
(1)第30个拐点处的数是多少?
(2)前30个拐点处的各数之和是多少?
【答案】(1)241.(2)2630.
【解析】
试题分析:第1个拐点处的数是1+1=2,第3个拐点处的数是1+1+3=5,第5个拐点处的数是1+1+3+5=10,…,可得当n为奇数时,第n个拐点处的数是:1+(1+3+5+…+n);第2个拐点处的数是1+2×1=3,第4个拐点处的数是1+2×(1+2)=7,…,可得当n为偶数时,第n个拐点处的数是:1+2×(1+2+3+…+![]() );
);
(1)第30个拐点处的数是:1+2×(1+2+3+…+15),据此解答即可;
(2)分别求出第1、2个,第3、4个,…、第29、30个的拐点处的个数之和;然后相加,求出前30个拐点处的各数之和是多少即可.
解:根据分析,可得
当n为奇数时,第n个拐点处的数是:1+(1+3+5+…+n);
当n为偶数时,第n个拐点处的数是:1+2×(1+2+3+…+![]() );
);
(1)第30个拐点处的数是:
1+2×(1+2+3+…+15)
=1+2×120
=241;
答:第30个拐点处的数是241.
(2)根据n为奇数、偶数时,第n个拐点处的数的表达式,可得
第1个、第2个拐点处的数的和是:1+1+(1+2)=5,
第3、4个拐点处的各数之和是:1+1+(1+2+3+4)=12,
第5、6个拐点处的各数之和是:1+1+(1+2+3+4+5+6)=23,
第7、8个拐点处的各数之和是:1+1+(1+2+3+4+5+6+7+8)=38,
…,
第29、30个拐点处的各数之和是:1+1+(1+2+3+4+…+29+30)=467,
因为12﹣5=7,23﹣12=11=7+4,38﹣23=15=11+4,…,
所以每个和与它前面的和的差分别是7、11、15、…,
它是一个首项是7,公差是4的等差数列,
因此前30个拐点处的各数之和是:
5+12+23+38+57+80+107+138+173+212+255+302+353+408+467=2630.
答:前30个拐点处的各数之和是2630.

 中考解读考点精练系列答案
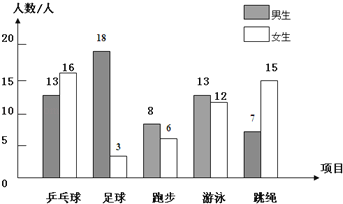
中考解读考点精练系列答案【题目】如图是我国2001﹣﹣2004年废水排放量统计图.

根据统计图完成统计表:
年份 排放量/亿吨 名称 | 2001 | 2002 | 2003 | 2004 |
工业废水 | ||||
生活废水 |
(1)我国工业废水排放量从2001﹣﹣2004年发生了怎样的变化?
(2)我国生活废水排放量从2001﹣﹣2004年发生了怎样的变化?
(3)根据图中的信息,谈谈你的想法.